傅里叶级数和傅里叶变换是什么关系?
27 个回答
之前写过两篇关于傅立叶变换的文章:
- 如何直观地理解傅立叶变换?
- 如何理解傅立叶级数公式? (后面此文简称“代数细节”)
傅立叶级数是针对周期函数的,为了可以处理非周期函数,需要傅立叶变换。如果对傅立叶级数有疑问,请参看“代数细节”一文。
先看下思路:
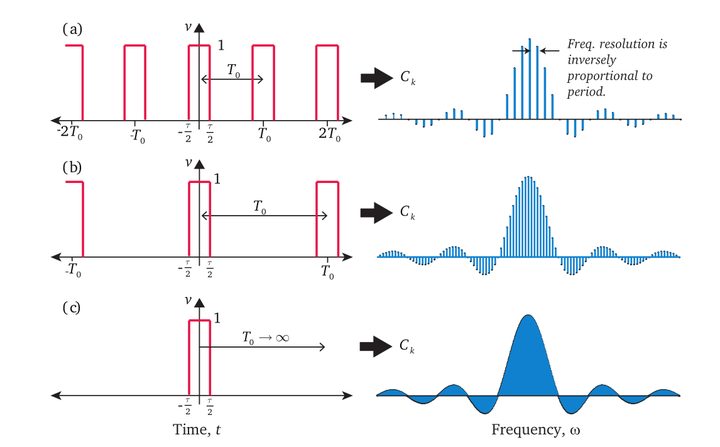
- (a).周期函数,可以通过傅立叶级数画出频域图
- (b).增长周期,频域图变得越来越密集
- (c).
,得到傅立叶变换,频域图变为连续的曲线
下面是细节的讲解。
1 傅立叶级数
让·巴普蒂斯·约瑟夫·傅里叶男爵(1768 -1830)猜测任意周期函数都可以写成三角函数之和。比如下面这个周期为 的方波,可以用大量的正弦波的叠加来逼近:
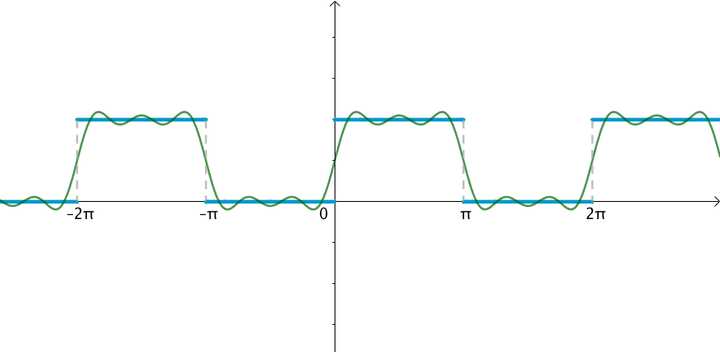
1.1 傅立叶级数是向量
从代数上看,傅立叶级数就是通过三角函数和常数项来叠加逼近周期为 的函数
:
在“代数细节”一文中解释了,实际上是把 当作了如下基的向量:
那么上面的式子就可以解读为:
说具体点,比如刚才提到的, 的方波
,可以初略的写作:
从几何上看,有那么一丁点相似:

我们可以认为:
此函数的基为:
则 相当于向量:
画到图上如下,注意坐标轴不是 ,而是
:

1.2 频域图
再增加几个三角函数:
从几何上看,肯定更接近了:

此时基为:
对应的向量为:
六维的向量没有办法画图啊,没关系,数学家发明了一个频域图来表示这个向量:

上图中的 分别代表了不同频率的正弦波函数,也就是之前的基:
而高度则代表在这个频率上的振幅,也就是这个基上的坐标分量。
这里举的例子只有正弦函数,余弦函数其实也需要这样一个频谱图,也就是需要两个频谱图。当然还有别的办法,综合正弦和余弦,这个后面再说。
原来的曲线图就称为时域图(这点请参考“代数细节”),往往把时域图和频域图画在一起,这样能较为完整的反映傅立叶级数:

不管时域、频域其实反映的都是同一个曲线,只是一个是用函数的观点,一个是用向量的观点。
当习惯了频域之后,会发现看到频域图,似乎就看到了傅立叶级数的展开:
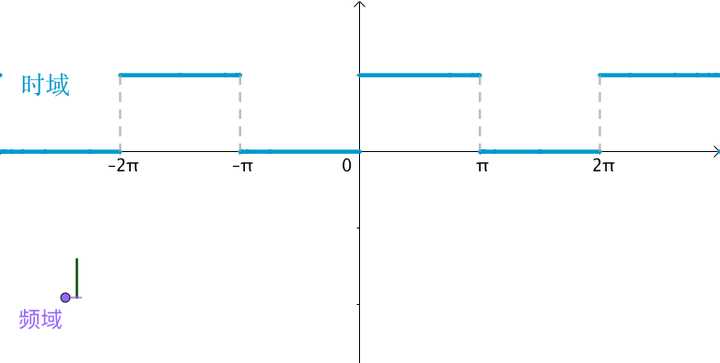
2 非周期函数
非周期函数,比如下面这个函数可以写出傅立叶级数吗?

这并非一个周期函数,没有办法写出傅立叶级数。
不过可以变换一下思维,如果刚才的方波的周期:
那么就得到了这个函数:
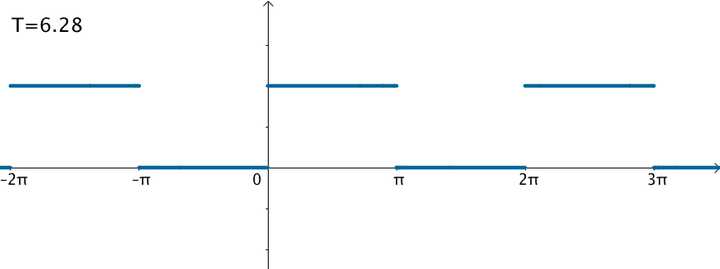
在这样的思路下,就可以使用三角级数来逼近这个函数:
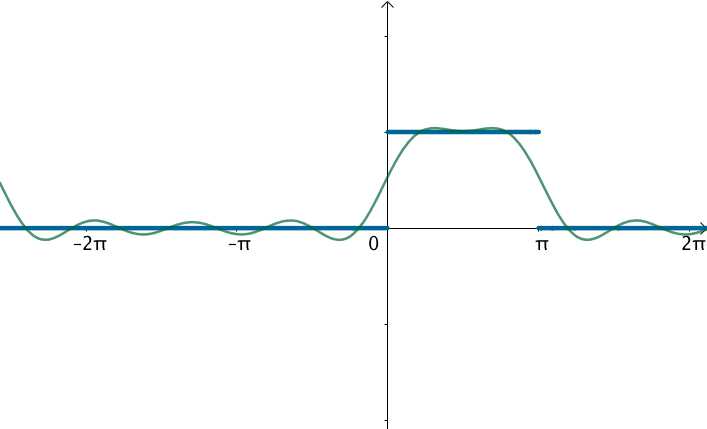
观察下频域,之前说了,对于周期为 的函数
,其基为(对此点有疑问的,可以看“代数细节”一文):
刚才举的方波 ,对应的基就为(没有余弦波):
对应的频率就是:
按照刚才的思路,如果 不断变大,比如让
,对应的基就为(没有余弦波):
对应的频率就是:
和刚才相比,频率更加密集:
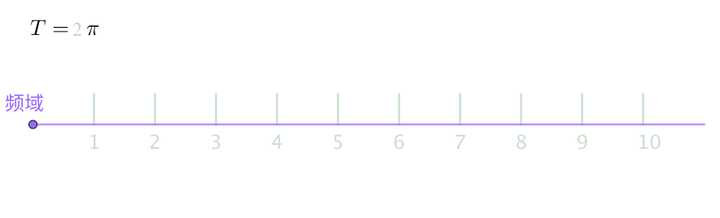
之前的方波的频域图,画了前50个频率,可以看到,随着 不断变大,这50个频率越来越集中:
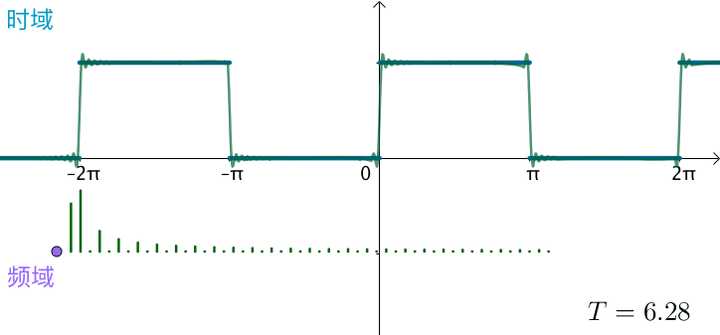
可以想象,如果真的:
这些频率就会变得稠密,直至连续,变为一条频域曲线:

傅立叶变换就是,让 ,求出上面这根频域曲线。
3 傅立叶变换
之前说了,傅立叶级数是:
这里有正弦波,也有余弦波,画频域图也不方便,通过欧拉公式,可以修改为复数形式(请参考“代数细节”一文):
其中:
复数形式也是向量,可以如下解读:
不过 是复数,不好画频域图,所以之前讲解全部采取的是三角级数。
周期推向无穷的时候可以得到:
上面简化了一下,用 代表频率。
大致是这么得到的:
就是傅立叶变换,得到的就是频域曲线。
下面两者称为傅立叶变换对,可以相互转换:
正如之前说的,这是看待同一个数学对象的两种形式,一个是函数,一个是向量。
广告时间:
傅立叶级数、傅立叶变换通过线性代数,更好理解。有兴趣学习线代基础的同学,可以参加我们的“线代基础课程”(报名方法:关注微信公众号:马同学高等数学,公众号ID:matongxue314,点击菜单栏的“线代课程”)。
文章最新版本在(有可能会有后续更新):从傅立叶级数到傅立叶变换


结合自己的理解写点。
这个帖子分三个部分,第一部分为怎么从傅里叶级数推导出傅里叶变换,第二部分为两者的联系 ~~第三个为通过傅里叶级数求取傅里叶变换的例子。
不好意思我update了,后面还加了一些内容。
[19/04/2017] 看到大家继续点赞,那我再加点有关傅立叶级数的理解吧,本应当放到第一节,但是因为公式都编号了,不想改了。
- 正交函数基的概念
- 傅立叶级数和正交多项式级数
- 正交多项式和泰勒级数展开
- 正交概念、级数展开在工程中的应用
- 【19/04/2017】傅立叶级数的直观理解
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
傅里叶变换的由来
傅里叶级数适用于周期信号中,下面给出其表达式:
(1)
(2)
周期的意义在于限定傅里叶系数的积分公式 (如(2)所示) 的积分上下限,把公式(1)代入到(2)中可以发现,(2)式子左右恒等,其中利用到了e指数的正交性。
那如果是非周期信号呢?公式(1)中的都已经不存在了(或者说是无穷小),此时时域信号便不可能写成如式子(1)级数的形式。但数学家们不甘心啊,如果把傅里叶只限定在周期信号,世界得多无趣啊。好,那就试着能不能重新定义非周期信号的傅里叶变换呢?数学家们思索着,这两种信号的区别在于一个是有固定的基频,另外一个基频无穷小。哎,等等?好像灵感来了,无限小的求和概念不就对应着积分嘛!那我们就尝试这能不能从这个角度来推导出非周期信号的傅里叶变换呢,好的,那我们试试吧。

考虑上述两个信号,对应为
的周期延展。对于
, 有
。对于周期信号
,对应的傅里叶系数为
(3)
现在定义为
的包络,其中的
用
来代替,注意,此处的定义只是一个notation的变化,没有改变方程任何的东西
(4)
显然,只是
的等间隔采样
(5)
注意,把傅里叶系数表示为包络的采样,应该算是数学家的直觉尝试,或者说是他们常用的技巧吧,因为取极限
有
, 方便后面进一步把级数转变成积分形式。其中没有把T集成
中,应该算是大家的约定吧,没办法,只能按照那些大牛的爱好了~ 好,那现在我们把公式(5)代入公式(1)中
(6)
(6)式中只含有和
, 此刻,数学家们开始笑了,万事具备,东风亦来,吼吼吼。 令公式(6)中的
, 也即
, 此时
, 哇~好熟悉的感觉,瞬间少女变大嫂~~ 公式(6)为
(7)
其中如公式(4)所定义~傅里叶级数的包络奥~在这里重新写下把
(8)
到了这里,数学家们才舒了一口气~~哈哈哈,攻城狮大笑,现在可以尽情灌水了~~~
=======================================================
傅里叶级数和傅里叶变换的关系
很多人说傅里叶技术用于周期信号,傅里叶变换用于非周期信号。那问题来了,周期信号的傅里叶变换是什么?并且和傅里叶级数的系数有什么关系?
为了解开这个谜团,我们先来热热身~来点预备知识。首先,周期信号可以由傅里叶级数表示,即e指数的求和形式,想到这一点,攻城狮开始猥琐的笑了起来,仿佛透视了对面的可爱妹子~~么么哒。。。周期信号的傅里叶变换的关键不就在于e指数的傅里叶变换嘛~~
直接给出e指数的傅里叶变换~
(9)
可以验证下~ 把(9)代入到 (7)式中
(10)
而对于周期信号可以表示为傅里叶级数
(11)
对周期信号进行傅里叶变换,即对公式(11)的e指数进行傅里叶变换~,借助公式(9),可以得到
(12)
可以看出,周期信号的傅里叶变换并不连续,并且都可以表示为一系列的脉冲叠加,其中脉冲前面的系数为, 即为 傅里叶系数的
倍。
=======================================================
通过傅里叶级数求取傅里叶变换的例子
最经典的例子莫过于脉冲采样理论了
对于采样系统中,我们一般采用脉冲去对信号进行采样,脉冲信号可以表示为
(13)
因为这是典型的周期信号,对应的傅里叶级数的系数为
(14)
根据公式(12)其傅里叶变换为
(15)
借助周期信号傅里叶系数和傅里叶变换的关系,可以很快求出周期信号的傅立叶变换。
==============================================
Update 一下有关正交展开吧。
Part 1: 正交函数基的概念
正交概念一般是定义在闭区间上的,假设这个闭区间为 , 那么对于两个函数
和
的正交,说的是其内积为零,如下面公式所示
(16)
假设函数列 是一组函数基,并满足
(17)
根据魏尔斯特拉斯逼近定理:
- 闭区间上的连续函数可用多项式级数一致逼近;
- 闭区间上周期为
的连续函数可用三角函数级数一致逼近.(其实可以用更加紧凑的方式表述:三角级数和多项式级数在C[a,b]中稠密)
可以知道闭区间上上的连续函数
可以用正交函数列
(多项式和三角级数) 来一致逼近
(18)
根据最优理论,我们考虑其平方误差积分最小
(19)
根据多维函数求极极值理论,上述式子(19)对 的导数等于零
(20)
根据勒贝格测度的控制积分理论,对于闭区间上的连续函数 ,如式子(20),其微分和积分符号可以交换顺序,详细参考我的实变函数Notes ,控制收敛定理84-85页。
http://pan.baidu.com/s/1kVJSHWN
于是有
(21)
进一步有
(22)
根据我们的正交假设(17)显然有如下结论
(23)
魏尔斯特拉斯定理的意义
显然我们可以用上述正交基对任意的连续函数函数去逼近,也总归会得到一个最优逼近下的一组系数 ,但是这个最优逼近是否能够无限逼近原函数?魏尔斯特拉斯定理的意义就在保证了多项式和三角级数可以一致逼近闭区间上的连续函数,也就是说当正交级数的项达到一定的数目时,在整个闭区间上无限逼近原函数了,严格来讲,就是闭区间上最大的逼近误差可以控制到任意小。
简而言之,闭区间上的连续函数可以等效为无数正交函数基(如傅立叶)的线性叠加,这样的好处就在于不同函数之间的区别现在量化成了不同的正交系数的区别,这种正交变换的好处是,打个比方,函数
类比成李雷家的猪,
类比为韩梅梅家的小麦,现在李雷想吃面粉,韩梅梅想吃肉,于是要想要交换下。但是他们并不知道这只猪该换几斤麦子啊,那好,现在有一个专门的机构,能够把不同物品使用统一种货币(正交基)来量化,于是下次见面直接说李雷的猪多少钱(
的傅立叶系数),韩梅梅家的麦子多少钱(
的傅立叶系数 ),这样大家就能够快速的有一个量化的比较了。
============================================
Part 2: 傅立叶级数和正交多项式级数
让这个正交函数基为 ,抑或(
),这就在理论上得到了傅立叶级数。
我们也可以探索把多项式作为我们的基 ,但是这组基并不是正交的,不过没关系,我们可以用格拉姆-施密特方法正交化,然后就得到了正交的多项式基,也就是勒让德多项式,如下图。

==============================================
Part 3: 正交多项式和泰勒级数展开
既然讲到了正交多项式,那么不妨多说两句。大家注意到公式(19),在闭区间上使用有限项的基来逼近一个函数,这是全局的逼近,我们思考和泰勒展开有什么不同,泰勒展开只是在某个点附近逼近,当展开的级数越多,那么函数逼近的范围就越广。大家也许会注意到对于正交级数在闭区间上展开的系数使用积分来求取的,而泰勒展开的系数确是通过微分操作求取。
简而言之,正交级数(如勒让德级数)是全局的逼近,而泰勒展开是局域的。从上图可以看出,对于正交勒让德级数,从 到
维,需要全部计算前面所有的系数,所以随着
的增加,正交级数也越来越复杂(这句话的理解是把勒让德级数整理成泰勒级数的样子,那么会发现,每增加一个维度,所有多项式前面的系数都会变化,意味着这些系数重新算过了)。但是对于泰勒级数,每增加一个维度,只需要计算增加的那个维度的导数即可,前面基的系数都不用变。
==============================================
Part 4: 向量正交
我们回顾下公式(16)
如果我们把区间 离散化, 在里面采样
个点,那么
就相应变成了
维度的向量了,积分也就成了离散和,也就是内积了,(16)可以变为
(24)
那么正交的含义也就顺理成章地成了
(25)
所以,函数正交定义的形式和向量正交其实是内恰的,对于线性代数中的向量之间的投影同样可以类比到函数空间中,线性代数中的格拉姆-施密特正交化方法也就可以同样适用于函数基的正交化。把上述正交函数的概念类比到离散的代数空间,我们就从傅立叶级数顺理成章推广到了离散傅立叶变换DFT。
可以参考一个帖子
如何通俗地解释什么是离散傅里叶变换? - psyduck 的回答 - 知乎
Part 4: 正交概念、级数展开在工程中的应用
我只说我接触过的
- 对于通信的CDMA编码,Spread code是一系列的正交码,每个人分配一个这样的spread code作为身份的验证, 且这些码相互之间正交,所以我们接受到基站传回来的信息时,通过内积方式可以唯一解出属于自己的那部分信息,而不用担心别人的信息对自己信息的串扰。
- 对于通信的OFDM,本质上是把高速率的信息流拆分成若干的低速率信息流,然后通过载波聚合的方式正交地加载在同一个载波上,接收端通过积分就可以恢复这些信息,然后把多个低速率的信息流恢复为告诉串行的高速数据流。不同的通信编码方式,其共同点就是正交。
- 在电路理论中,泰勒级数和傅立叶级数也用的非常多,这俩好基友是非线性电路分析的不二法宝。很多非线性电路如功率放大器,整流电路的效率,输出功率的计算,无不利用到了这些级数。还有一些微波半导体器或者系统件行为建模方法,也是用到了这些技术。更加复杂的就是从一维变量的拓展到高维了。




傅里叶级数是周期信号的时域表达式,而傅里叶变换是非周期信号或周期信号的频谱(频域函数),要想了解它们之间的关系,需要你耐心看完下面内容。
学过"信号与系统"等课程的人往往会被许多问题所困惑,如:
(1)周期信号傅里叶级数表示什么内容?
(2)信号的频谱表示什么?
(3)通过信号的频谱我们能知道什么?
(4)信号的时域和频域的关系是什么?
(5)傅里叶级数、傅里叶系数、傅里叶变换的关系是什么?
(6)周期信号傅里叶级数中的傅里叶系数物理意义是什么?
(7)周期信号傅里叶级数中的傅里叶系数与非周期信号傅里叶变换的关系是什么?
(8)非周期信号的傅里叶变换到底是什么意思?
(9)傅里叶变换的物理意义是什么?
(10)复数形式的傅里叶变换的物理意义?
(11)为什么周期信号的傅里叶变换在相应频率处出现冲激函数?
(12)为什么正弦(或余弦)信号的傅里叶变换是冲激函数?
上述问题尽管看上去有些零碎,其实它们是有联系的,下面,我从头到尾把这些问题串起来,内容可能比较多,如果你想知道结果,则需要你耐心阅读,并希望下面的内容能对你有所帮助,更详细的内容和应用还请参见我写的《信号与系统分析和应用》一书,本书在高等教育出版社出版发行。
如果你手里有《信号与系统分析和应用》教材,请你关注“信号与系统分析”微信公众号,那里面列出书中发现的问题。
要知道傅里叶变换把时域信号变换为频域函数(频谱),首先需要知道信号的频谱是什么。我在教学的时候,规定时域是“信号”,频域是“函数”。
注意,下面我站在求解“频谱”的角度来说问题!
一、周期信号及其频谱
1、先从周期信号说起
周期信号的频谱表示了这个周期信号含有的所有不同频率余弦信号的频率、幅度和初相位这三个“参数”,每个余弦的这“三个参数”表征了这个余弦的全部信息,信号的频谱是用原周期信号含有的所有各个频率余弦信号的“三参数”来表征原时域信号的组成成分和分量(傅里叶级数是在时域用余弦信号的形式来表征周期信号的组成。注意:傅里叶级数是时域的,它的自变量是时间t)。
我们不能总是喋喋不休地只讨论一个复杂的时间信号是由哪些基本信号合成的,而我们真正要关心的是这个复杂信号的“组成成分”和这些“成分的分量”。我非常赞赏网友用的“配方”这个词,它一针见血地指出了一个混合物(相当于时域信号)和它的组成成分及其分量(频谱---信号配方)。可以看到,周期信号的“配方”就是组成这个周期信号的各个频率的余弦的“频率”、“幅度”和“初相位”这“三个参数”。
如一副中药相当于原时域信号,而它的“药单”相当于其“频谱”。
一副混合好的中药(相当于一个复杂信号),你从下面图中看不出组成它的各成分的分量。

要想知道它的组成成分和分量,你一定要拿到它的药单。

药单上列出了一副中药的组成成分和各味药的“分量”。对应我们讨论的信号来说,药名相当于“余弦信号的频率”,重量相当于“余弦信号的幅度”。可以看到,这个药单图只有“各个味药”和它的重量,这个药单其实相当于“信号的幅度谱”。我们也可以把各味药的产地标上(也可以理解为余弦信号的初相位)。反过来,我们按着“药单”去抓药就能构成一副中药。
2、傅里叶积分公式(对非周期信号来说就是它的傅里叶变换)的伟大之处在哪里?
在这里为什么我要说“傅里叶积分公式”而不说“傅里叶变换”?因为,求周期信号的频谱是用傅里叶积分公式,而求非周期信号的频谱的公式我们通常称其为“傅里叶变换”,其实,傅里叶变换也是傅里叶积分公式。
傅里叶积分公式的伟大之处在于:利用信号的“正交性”,通过积分公式能求出原信号的“配方”或者说求出组成原信号所有不同频率余弦(或正弦)信号的“三参数”,也就是我们在信号与系统课程中讲到“频谱”。
傅里叶积分公式要完成两个任务:第一个是利用信号的“正交性”,从一个“混合物”(一个复杂信号)中分离出其中的一个成分(某个频率的余弦),另一个是它像一杆秤似的称出被分离出来的那个成分的“分量”(余弦的幅度和初相位)。我们不但要知道一个混合物的“成分”,还要知道其中某个成分的“分量”。所以,傅里叶积分公式兼有“成分分离器”和“秤”的双重作用。
下面就让我们去看看如何从复杂信号中分离出一个余弦,然后怎样求出被分离出来的这个余弦的幅度和初相位(这是一个真正伟大的工作)。
3、周期信号的表示以及它的频谱的求解
我们先看看一个周期信号的时域表示(傅里叶级数),然后就让我们去见证一个伟大的傅里叶积分公式,它是如何求出这个周期信号的“配方”(频谱),也就是用傅里叶积分公式如何从周期信号中分离出一个余弦以及怎样求出这个余弦的幅度和初相位的(这是一个真正伟大的工作)。
(1)周期信号三角函数形式的傅里叶级数
为了尽快完成下面内容,下面我把我写的《信号与系统分析和应用》书上内容直接复制过来,更详细内容还请参见这本书。
请注意:为什么我把周期信号三角函数形式的傅里叶级数写成下面的形式,而不是公式(4.2-8)的形式?因为只有这样才能充分理解信号频谱以及频谱的作用、傅里叶系数、非周期确知信号的傅里叶变换的物理意义,才能充分理解我写的下面的内容。

特别要注意:所谓的傅里叶级数是在时域用不同频率的余弦信号或正弦信号来表示原周期信号的组成。
由公式(4.2.2)可知:



这样就能计算出一个周期信号的频谱了(“配方”或“药单”)。我们将所有“三参数”按频率的位置表示出来就是原周期信号的“频谱”了,因此,下面的周期信号的傅里叶级数公式才是与“频谱”对应的周期信号三角函数形式的傅里叶级数。

用上面公式表示周期信号三角函数形式的傅里叶级数才能更好地理解信号的“频谱”到底表示了什么?以及后面我要说的非周期信号傅里叶变换的“物理意义”是什么,才能更好理解信号频域分析的目的。那么,公式(4.2-8)可以看做求解信号频谱的中间环节,当然,它也是三角函数形式的傅里叶级数,只是用它不利于理解信号频谱表示的内容(也有特殊情况)。
可以说,公式(4.2-10)以及(4.2-11)是“最伟大的积分公式”之一。这两个公式为什么能计算出an和bn?我们需要讨论信号的正交性问题。
下面把《信号与系统分析和应用》书上内容复制过来。

注意:上面积分区间一定在是整倍周期期间才成立。


这样,下面的积分公式的物理意义就很清楚了:




想必大家已经领略到了数学的伟大魔力了吧。
4、周期信号组成成分的表示---信号频谱


可以看到,频谱图(a)和(b)表示了组成原周期信号的所有不同频率余弦信号的“频率”(横坐标)、“幅度”以及“初相位”这三个参数,这与公式(4.2.2)是对应的,这就是为什么我将周期信号傅里叶级数写成公式(4.2.2)的根本原因。
信号频谱的作用就是用图形(频谱图)或公式(向量形式)来表示组成这个周期信号的所有不同频率的余弦信号的“三参数” (幅度、初相和频率或角频率),也就是说,频谱是用“参数”的形式表示原信号的组成成分,我们不但要知道信号的组成成分还要知道这些成分的份额,这就是大家说到的“原信号的配方”。从频谱图上,我们就能看到原周期信号含有的所有频率的余弦(或正弦)信号的幅度和相位的大小,也就知道了周期信号含有的所有频率成分以及这些频率成分对原信号的贡献大小。上面图(c)是将图(a)和(b)合成一个图(合成的原则请参见《信号与系统分析和应用》书)。
周期信号的傅里叶级数是在时域用不同频率的余弦信号或正弦信号来表示原周期信号的组成,而周期信号的频谱是用“参数”的形式表示这个周期信号的组成成分。
5、周期信号复指数形式的傅里叶级数与信号频谱



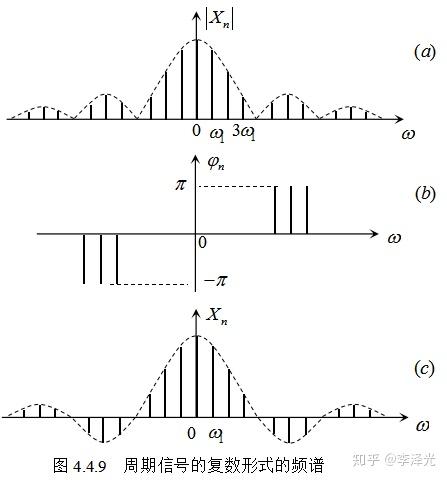
周期信号复指数形式傅里叶级数中的傅里叶系数Xn是用复数的形式表示每个余弦信号的幅度和初相位信息(包含余弦信号的两个参数)。
一定注意:傅里叶系数Xn的积分公式其实还是求an和bn(系数为0.5),只是用一个积分公式的实部和虚部一起求出的,它还是利用“正交性”,傅里叶系数Xn就是复数形式的原周期信号的“频谱”(“药单”或“配方”)。
特别强调一下:将傅里叶系数Xn的虚部看成是余弦信号的初相是不对的,它的虚部0.5bn是“正弦分量”的幅度信息,不是余弦信号的初相位,而余弦信号的初相是公式(4.4-17),下面讨论非周期信号傅里叶变换也是这个问题,即绝对可积非周期信号的傅里叶变换是一个复函数,它的虚部也不是任意角频率w的余弦信号的初相位。
二、非周期信号的傅里叶变换
非周期信号的傅里叶变换是从周期信号复指数形式傅里叶级数中的傅里叶系数Xn推导来的(注意:不是从傅里叶级数推导来的!),所以,非周期信号的傅里叶变换就是非周期信号的“频谱”。
绝对可积信号的傅里叶变换是自变量为频率或角频率的复函数,它含有原时域信号含有的所有频率余弦信号的“三参数”信息(频率信息是由傅里叶变换的自变量来表征的),它是一个复函数(他跟周期信号傅里叶级数中的傅里叶系数Xn的物理意义相似),它的实部表示原信号含有的任意角频率w余弦信号的同相分量(余弦分量)的幅度信息,其虚部表示信号含有的任意角频率w余弦信号的正交分量(正弦分量)的幅度信息。但是,绝对可积非周期信号含有的每个余弦信号的幅度都趋于无穷小,非周期信号的傅里叶变换中的幅度谱是每个余弦信号无穷小的幅度乘上一个无穷大的周期。如果一个非周期信号是确知信号,则它的傅里叶变换就是一个自变量为频率或角频率的确知相量函数(所以,不能把它叫做信号),这说明,这个原确知时间信号含有的所有频率余弦信号的幅度和初相不是孤立的,他们满足一定关系,这个关系就是以自变量为频率或角频率的“频域函数”。更多内容请参看我写的《信号与系统分析和应用》书上第4章和第5章内容。



下面举个信号的例子:


上面是信号傅里叶变换是复函数的物理意义。下面看看因果稳定系统的频率响应的物理意义。
因果稳定系统的频率响应是此系统单位冲激响应的傅里叶变换,由于此系统是因果稳定系统,则其频率响应也是复函数。

可以看到,信号的傅里叶变换与系统单位冲激响应的傅里叶变换即使都是复函数,但是,它们的物理意义是不同的。
三、周期信号的傅里叶变换以及冲激函数的作用


如果你手里有《信号与系统分析和应用》教材,请你关注“信号与系统分析”微信公众号,那里面列出书中发现的问题。
目前,已开始逐渐把我主讲的“信号与系统”视频课上传到B站上的“李泽光老师”主页上,欢迎你关注并提出意见和建议。


傅里叶变换是对 “直线加群” 上函数的傅里叶变换;
傅里叶级数是对 “圆周群” 上函数的傅里叶变换;
在抽象的理论中我们可以把傅里叶变换定义到局紧交换群上的函数上去。
(积分由幺模群上哈尔测度给出)






