形象理解二维傅里叶变换
2020/3/3更新,增加了一些公式,准确了一些用语,调整了一下回答的逻辑。
--------------------------------------------------------------------
1.回顾一下一维FT
公式:
通俗来讲,一维傅里叶变换是将一个一维的信号分解成若干个复指数波 。而由于
,所以可以将每一个复指数波
都视为是余弦波+j*正弦波的组合。
对于一个正弦波而言,需要三个参数来确定它:频率 ,幅度
,相位
。因此在频域中,一维坐标代表频率,而每个坐标对应的函数值也就是
是一个复数,其中它的幅度
就是这个频率正弦波的幅度
,相位
就是
。下图右侧展现的只是幅度图,在信号处理中用到更多的也是幅度图。
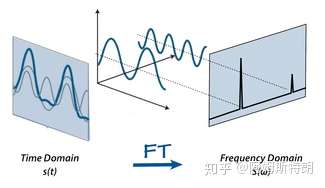
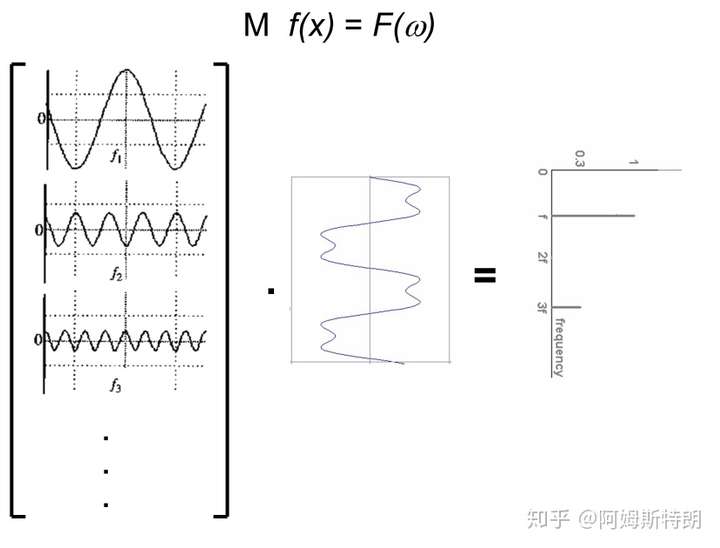
一维傅里叶变换就是一个基变换,在时域中,基是一族冲激信号 ,在频域中;基是
,而且这组基是正交基。
2.类比:从一维到二维
一维信号是一个序列,FT将其分解成若干个一维的简单函数之和。二维的信号可以说是一个图像,类比一维,那二维FT是不是将一个图像分解成若干个简单的图像呢?
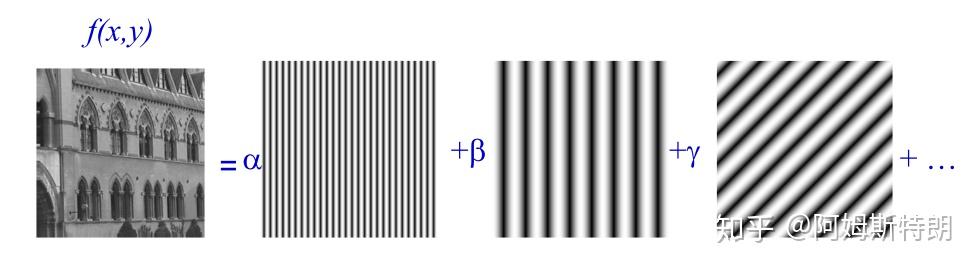
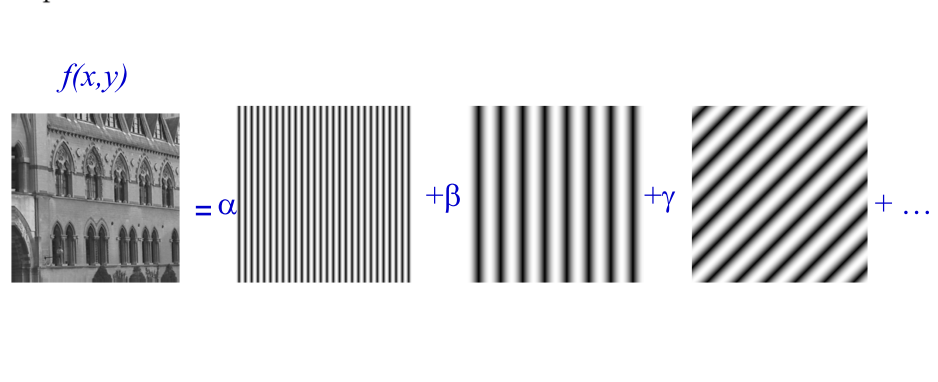
确实是这样,二维FT将一个图像分解成若干个复平面波 之和。如下图:
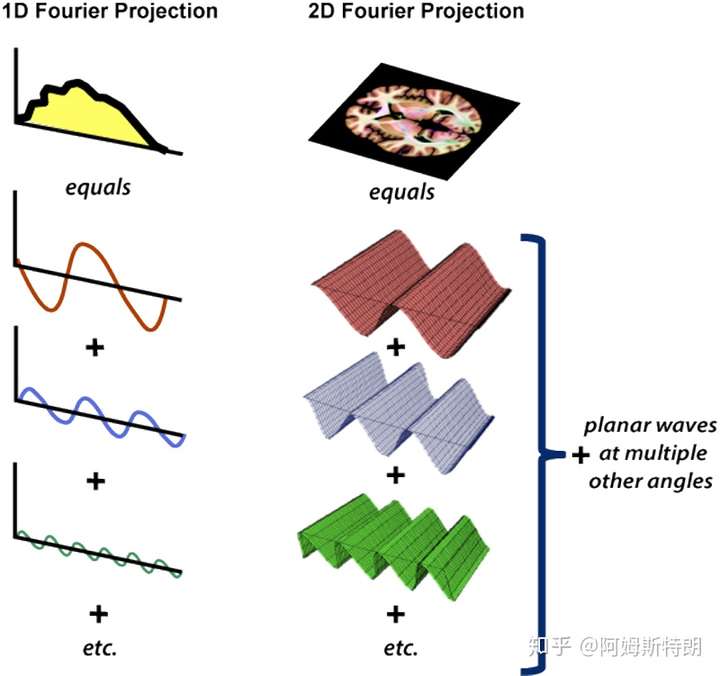
- 二维FT的公式:
通过公式,我们可以计算出,每个平面波在图像中成分是多少。从公式也可以看到,二维傅里叶变换就是将图像与每个不同频率的不同方向的复平面波做内积(先点乘在求和),也就是一个求在基 上的投影的过程。(应该知道
是b在a上的投影,只不过这里的|a|的值被设为1,所以只有内积)
3.什么是二维频率域K-SPACE
对于正弦平面波,可以这样理解,在一个方向上存在一个正弦函数,在法线方向上将其拉伸。前面说过三个参数可以确定一个一维的正弦波。哪几个参数可以确定一个二维的正弦平面波呢?答案是四个,其中三个和一维的情况一样(频率 ,幅度
,相位
),但是具有相同这些参数的平面波却可以有不同的方向
。如下图所示:
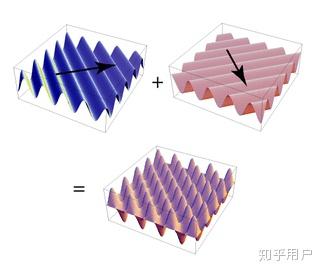
类比一维中,幅度和相位可以用一个复数表示,它可以作为我们存储的内容。但是还有两个:一个频率一个方向。这时想到向量是有方向的,也是有长度的。所以我们用一个二维的矩阵的来保存分解之后得到的信息。这个矩阵就是K空间。(一般用k来表示空间频率,单位是1/m)
什么意思呢?就是说一个二维矩阵点 代表这个平面波的法向量
,这个向量的模
代表这个平面波的频率
,这个点里面保存的内容复数就是此平面波的幅度和相位。下面这个图很好的体现了这一点:
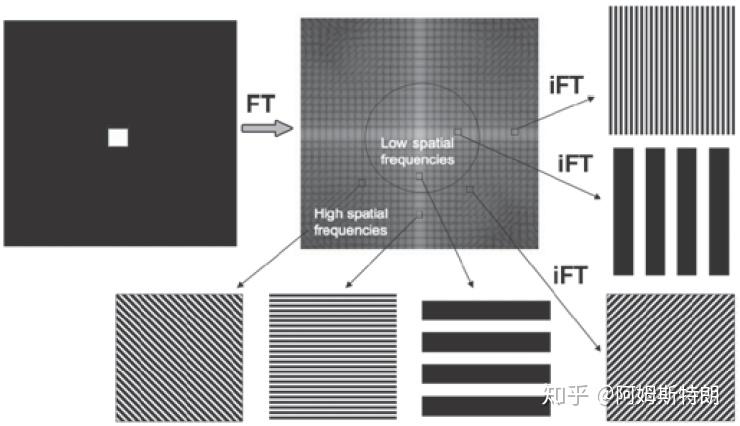
也因此K空间的中心对于低频,周围对于高频。如下图,K空间中只有(0,0)处有值,也就是信号都是直流即不存在变化,所以实空间就是一张白纸。

再如下面这个图片,中心低频贡献了图像的主体,周围高频提供图像的细节和边缘。

因此,k空间的每一个位置存储的数代表了所在位置复平面波在图像中占多少成分,我们就可以用每个系数*所代表的平面波相加得到原来的图像,也就是下图。所以k空间和对应图像储存的信息含量是一样的,只不过表现形式不同,或者说基不同。
4.K空间的一些性质
- 离散的2D-FT
在数字图像中,数据都是离散的。也就涉及到采样的问题,和一维一样,如果采样率过低,k空间就会混叠。同时在k空间中采样过低,图像也会混叠。
FOV和分辨率在k空间和图像中是相反的关系。也就是:
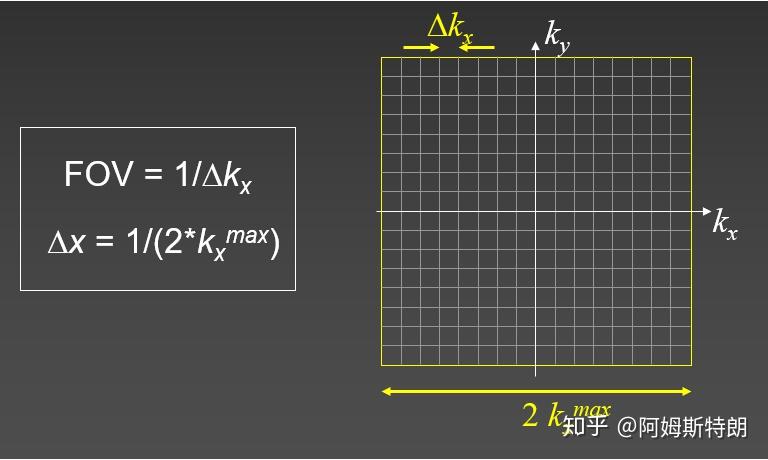
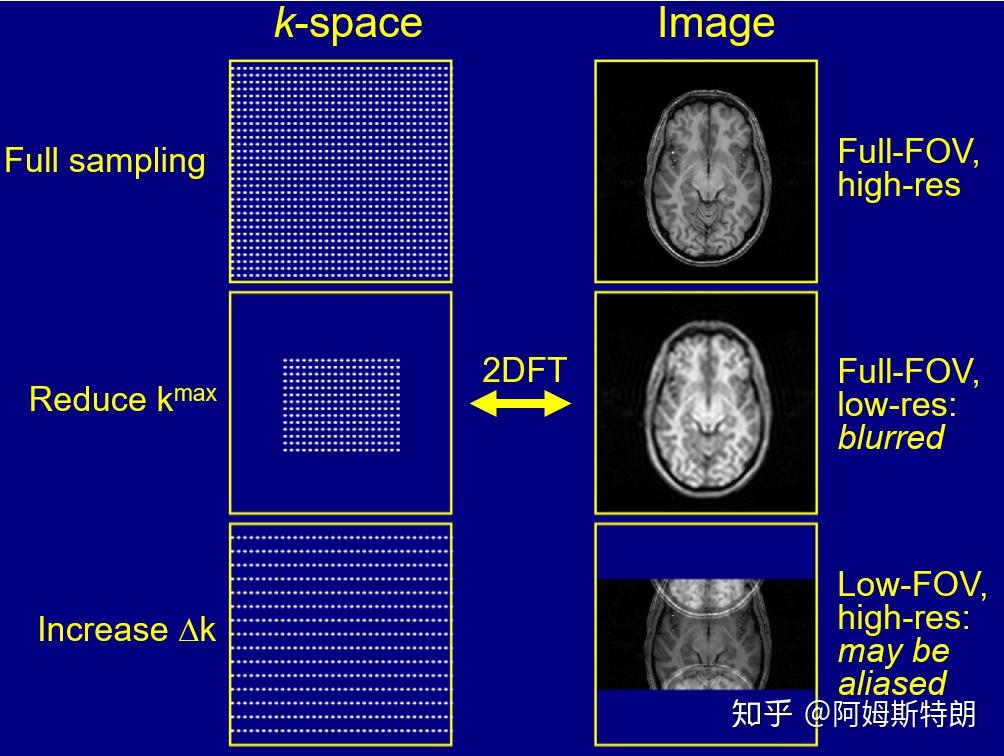
- 旋转不变性。
从平面波的角度很容易理解,旋转没有改变平面波的幅度相位,只是将所有的平面波都旋转了一个角度。下面这个图像显示了二维傅里叶变换中,实空间旋转多少,频率空间也会相应旋转多少。这其实是高维傅里叶变换缩放定理的一种特殊情况。(连续的是可以证明的,离散的涉及插值 ,不一定完全准确)

5.其他
1.因为matlab中的fft算法都是将0放在第一个的,所有写matlab时一定要将k空间fftshift一下使得零频回到k空间中心。
2.简单的应用k空间进行去噪例子。通过去掉明显的k空间的异常峰,可以去除图像中有规律变化的噪声或者伪影。


6、评论及解答
1、始终想不通为啥各个波的叠加能反应出某一个像素点的信号大小
你把它理解向量分解就懂了,平面波就是基,k空间里的数就是基的系数。你得到系数(k空间)的时候就是在投影,变为原向量(图像)就是叠加。只不过这里一个图像是一个向量而已。复平面波叠加时,先经过放大(幅度)在经过移位(相位),相位信息里保留了很多位置信息,可以查看我的另一个回答:
为什么用图像二维傅里叶变换的相位谱进行反变换,能够大致得到原图的形状,而幅度谱则不行呢?
2、傅里叶变换后图像是关于频率矩形中心对称的,那么对称的4个平面三角波不就是注定了幅值和相角,频率是相等的。那么这样不是说明了任何波都是包含了4个这样对称的三角波,由它们组成?
是中心共轭对称,而没有左右上下的对称。而且只有实数图像的k空间才有这种特点,这是为了将复平面波中的虚部抵消掉,只留下实数部分。复数图像的k空间没有共轭对称的特点。下面是k空间的一部分数据,中心点为(101,101)。
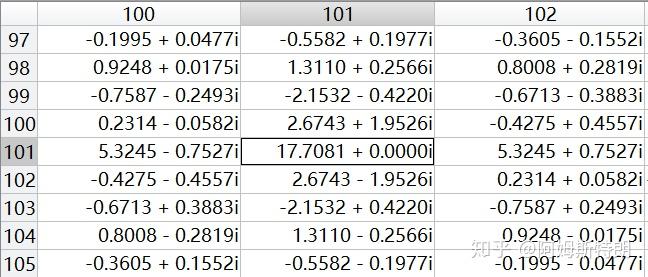
参考:
[2] A. Zisserman's lecture in B14 Image Analysis(这个slides真的不错,大家可以下载看看,里面也有其他的内容)


29 条评论
写的很好,本质上高维空间RN上的FT都是这个道理,分解为空间上不同k方向上的单向周期性场,另外我觉得Stein的Fourier analysis an introduction写的很好,需要了解的可以参考。而且事实上除了信号处理,在固体力学和复合材料力学中,FT的用处也非常多 :)
写的太形象生动了!反正我是个小白,你怎么讲,我也不知道数学符号是啥意思。只知道图片很美~~~
哈哈,数学是美的。
换句话说,从图像处理的角度来看,K空间是MRI图像的频域表征,但是从MRI物理上来讲,K空间数据其实是一组时域信号。这个容易引起混淆,最好就是在解释图像的二维傅里叶变换时不要使用MRI图像做例子。
用mri的例子确实容易引起误导。
想咨询一下答主,图像的卷积和傅立叶变换有关系吗?
大佬你好,我在对多道波用MATLAB自带的二维傅里叶函数处,可以得到频率谱和相位谱,我想问一下如何实从相位谱转化为一情况下的波数k,然后利用频率除以波数得到相速度?
那张频域细节的图真实太顶了,怒赞博主
请问二维傅里叶变换后的横纵坐标分别代表什么呢
那个基的说法不对,f(x,y)的基是e^{j2\pi (ux+vy)},而不是e^{-j2\pi (ux+vy)}。可以认为F(u,v)的基是e^{j2\pi (ux+vy)}。
二维傅里叶变换可以理解为描述物体表面的光滑度。
非常感谢答主如此细致入微的解答!学生一枚,关于图像频谱里面(u,v)究竟是什么意义真是困扰我很久了,今天在您的答案这里终于解惑了,感谢!