接黎曼猜想,及其解释(上)
黎曼的工作 现在基础资源已经齐备,我们终于可以建立起素数与黎曼猜想之间的联系了。
德国数学家波恩哈德·黎曼,1826 年生于布列斯伦茨。师从高斯的黎曼发表了分析与几何领域的工作。他最大的贡献在微分几何领域,为后来爱因斯坦在广义相对论中使用的几何语言奠定了基础。
他在数论中唯一的成就,论文 Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse,“论小于给定数值的素数个数”被认为是该领域中最重要的论文。他在短短四页中概述了:
黎曼 zeta 函数 ζ(s) 的定义,一个复值化的 zeta 函数; zeta 函数对于所有复数 s≠1 的解析延拓; 黎曼 xi 函数 ξ(s) 的定义,一个通过 Gamma 函数与黎曼 zeta 函数建立起联系的整函数; 黎曼 zeta 函数的两个函数方程的证明; 黎曼素数计数函数 J(x) 的定义,通过素数计数函数和莫比乌斯函数定义; 通过黎曼 zeta 函数的非平凡零点定义的黎曼素数计数函数,给出了一个明确的公式来计算小于给定数值的素数个数。 这是个令人难以置信的壮举!这种工程性和创造力大概从来没人见过。绝对惊人!
黎曼 zeta 函数 我们已经看到了欧拉在它的乘积公式中展示的素数个数与 zeta 函数之间的紧密联系。然而除了这种关联外,我们对它们的关系知道得并不多,而复数的引入则明确地展示了这二者之间是如何相互联系的。
黎曼是第一个对复变量 s 考虑 zeta 函数 ζ(s) 的人,其中 s = σ + it。
<img src="https://pic4.zhimg.com/v2-1ffe0a0ebecf93bbaf554942bad9837b_b.jpg" data-caption="" data-size="normal" data-rawwidth="1400" data-rawheight="302" class="origin_image zh-lightbox-thumb" width="1400" data-original="https://pic4.zhimg.com/v2-1ffe0a0ebecf93bbaf554942bad9837b_r.jpg"/> 黎曼 zeta 函数对于 n,其中 s = σ + it 为复数,σ 和 t 均为实数。
被称为黎曼 zeta 函数的 ζ(s),是一个对所有实部大于 1 的复数(Re(s) > 1)解析(即有可定义的值)的无限级数,在这一区域内,它绝对 收敛。
为了分析规则收敛区域(即复变量 s 的实部大于 1)以外的区域中的函数,该函数需要重新定义。黎曼通过对 Re(s) > 0 半平面中绝对收敛的函数进行解析延拓,成功地做到了这一点。
<img src="https://pic4.zhimg.com/v2-7ee3f89a8395a32c88c3755b05f81ca7_b.jpg" data-caption="" data-size="normal" data-rawwidth="662" data-rawheight="180" class="origin_image zh-lightbox-thumb" width="662" data-original="https://pic4.zhimg.com/v2-7ee3f89a8395a32c88c3755b05f81ca7_r.jpg"/> 黎曼 zeta 函数的重写形式,其中 {x} = x -∣x∣
zeta 函数的新定义在除 s = 1 这一奇点/简单极点外的 Re(s) > 0 半平面上解析。 它在该定义域上叫做亚纯函数,因为它除了在简单极点s = 1处以外是全纯的(此定义域中每一个点的领域均可微分)。它也是被称为狄利克雷 L-函数的一个很好的例子。
黎曼在他的论文中并未就此止步。它用 Gamma 函数 Γ(z) 继续将他的 zeta 函数解析延拓到了整个复平面。为了保持本文的简洁,我不会在这里展示它的计算过程,但我强烈推荐你自己读一下,它展现了黎曼敏锐的直觉和高超的技术。它的方法利用了 Gamma 函数 Γ(z) 对复变量的积分形式和雅可比 theta 函数 ϑ(x),它们一同重写后会出现 zeta 函数。zeta 函数的解析式为:
<img src="https://pic4.zhimg.com/v2-b10fe7f4488b9b45caeec2c445bba63b_b.jpg" data-caption="" data-size="normal" data-rawwidth="1400" data-rawheight="177" class="origin_image zh-lightbox-thumb" width="1400" data-original="https://pic4.zhimg.com/v2-b10fe7f4488b9b45caeec2c445bba63b_r.jpg"/> 对于整个复平面的一个函数式 zeta 方程,除了 s = 0 和 s = 1 两处奇点
在此形式中,可以看出 ψ(s) 项比 x 的任何次幂减少得更快,因此该积分对 s 的所有值收敛。甚至更进一步,黎曼注意到如果用 1-s 代替 s,那么大括号中的第一项是不变的。这样做之后,黎曼就移除了 s=0 和 s=1 两处极点,进一步扩展了此方程的用途,并定义了无奇点的黎曼 xi 函数:
<img src="https://pic3.zhimg.com/v2-5d36f49befdcfd1361aa92c53921521a_b.jpg" data-caption="" data-size="normal" data-rawwidth="1270" data-rawheight="244" class="origin_image zh-lightbox-thumb" width="1270" data-original="https://pic3.zhimg.com/v2-5d36f49befdcfd1361aa92c53921521a_r.jpg"/> 黎曼 xi 函数 ξ(s)
黎曼 zeta 函数的零点 zeta 函数的根/零点(即当 ζ(s) = 0 时)可被分为两种类型,分别被称作黎曼 zeta 函数的“平凡”和“非平凡”零点。
实部 Re(s) < 0 时存在的零点 平凡零点即容易找到和解释的零点。它们在 zeta 函数的以下函数形式中最中意注意到:
<img src="https://pic2.zhimg.com/v2-b94d0db8b9dddefacb23b04688c18c49_b.jpg" data-caption="" data-size="normal" data-rawwidth="1400" data-rawheight="199" class="origin_image zh-lightbox-thumb" width="1400" data-original="https://pic2.zhimg.com/v2-b94d0db8b9dddefacb23b04688c18c49_r.jpg"/> 黎曼的函数式 zeta 方程的一个变体
当正弦项为零时,该乘积亦为零。kπ 处均是如此。因此,例如对于负偶数 s = -2n,zeta 函数为零。然而对于正偶数 s = 2n,零点会与 Gamma 函数 Γ(z) 的极点抵消。这在原始的函数形式中更容易看到,若你将 s = 2n 代入,那么该项的第一部分会是未定义的。
<img src="https://pic2.zhimg.com/v2-77ea99c227d3d461d41138788a2aff8d_b.jpg" data-caption="" data-size="normal" data-rawwidth="1400" data-rawheight="186" class="origin_image zh-lightbox-thumb" width="1400" data-original="https://pic2.zhimg.com/v2-77ea99c227d3d461d41138788a2aff8d_r.jpg"/> 因此,黎曼 zeta 在每个负偶数 s = -2n 处都有零点。它们是平凡零点,可在以下函数图像上看到:
<img src="https://pic4.zhimg.com/v2-aed1a895ea8a269562c8735d038d0567_b.jpg" data-caption="" data-size="normal" data-rawwidth="1400" data-rawheight="924" class="origin_image zh-lightbox-thumb" width="1400" data-original="https://pic4.zhimg.com/v2-aed1a895ea8a269562c8735d038d0567_r.jpg"/> 标出了 s = -2, -4, -6 等平凡零点的黎曼 zeta 函数 ζ(s)
实部 Re(s) > 1 时存在的零点 从 zeta 的欧拉乘积表示中,我们立刻就会发现 ζ(s) 在 s 的实部大于 1 的区域内不能为零,因为如果其因子之一为零,则收敛的无穷大乘积只能为零,而素数无穷性的证明否定了这一点。
<img src="https://pic4.zhimg.com/v2-9445f55bd7c59039380760cbeb07df27_b.jpg" data-caption="" data-size="normal" data-rawwidth="774" data-rawheight="314" class="origin_image zh-lightbox-thumb" width="774" data-original="https://pic4.zhimg.com/v2-9445f55bd7c59039380760cbeb07df27_r.jpg"/> 欧拉乘积公式
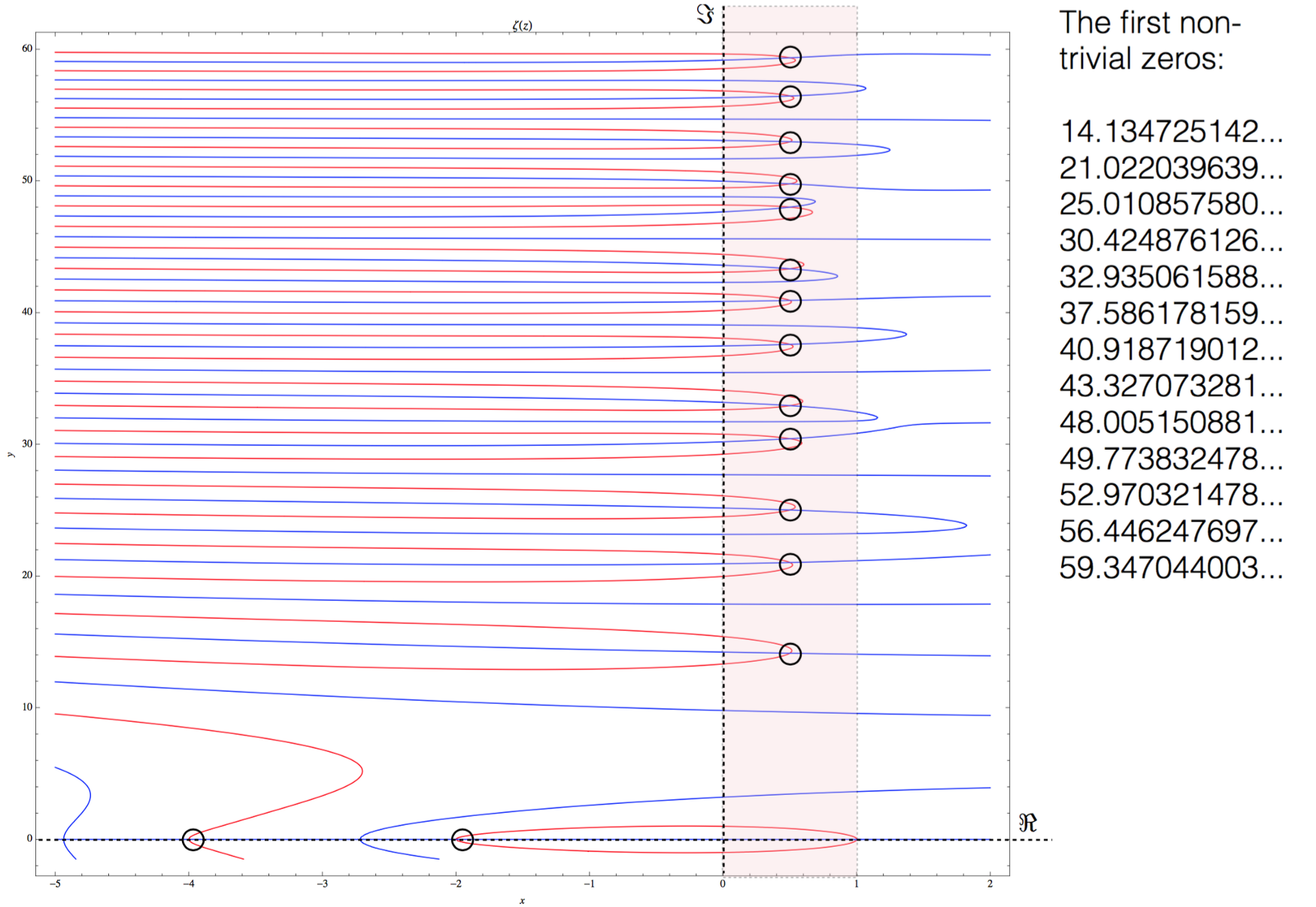
实部 0 ≤ Re(s) ≤ 1 时存在的零点 现在我们在 Re(s) < 0 的负半平面上找到了 zeta 的平凡零点,并展示了在 Re(s) > 1 的区域上不可能存在任何零点。然而在这两个区域之间,被称为临界带的区域,几百年来一直占据了分析数论的焦点。
<img src="https://pic2.zhimg.com/v2-f2aec999e829c0c77e21680b14cd21e9_b.jpg" data-caption="" data-size="normal" data-rawwidth="1750" data-rawheight="1206" class="origin_image zh-lightbox-thumb" width="1750" data-original="https://pic2.zhimg.com/v2-f2aec999e829c0c77e21680b14cd21e9_r.jpg"/> 黎曼 zeta 函数 ζ(s) 在区间-5 < Re < 2, 0 < Im < 60 内实部和虚部的图像
在上图中,我已经将 ζ(s) 函数的实部绘制成红色,虚部为蓝色。我们看到当s的实部为 -2 和 -4 时的两个零点在左下方。在0和1之间,我已经突出了临界带,并标出了 zeta 函数 ζ(s) 的实部和虚部相交的地方。它们是黎曼函数的非平凡零点。随着数值的升高,我们会看到更多零点,这两个看似随机的函数也随着s虚部的升高变得越来越稠密。
<img src="https://pic4.zhimg.com/v2-37634f10db21815f9c1ec7c49015e903_b.jpg" data-caption="" data-size="normal" data-rawwidth="1750" data-rawheight="1744" class="origin_image zh-lightbox-thumb" width="1750" data-original="https://pic4.zhimg.com/v2-37634f10db21815f9c1ec7c49015e903_r.jpg"/> 黎曼 zeta 函数 ζ(s) 在区间 -5 < Re < 2, 0 < Im < 100 内实部和虚部的图像
黎曼 xi 函数 我们已经将黎曼 xi 函数 ξ(s)(移除了奇点的函数方程版本,因此它在s的所有值上定义)定义为:
<img src="https://pic3.zhimg.com/v2-5d36f49befdcfd1361aa92c53921521a_b.jpg" data-caption="" data-size="normal" data-rawwidth="1270" data-rawheight="244" class="origin_image zh-lightbox-thumb" width="1270" data-original="https://pic3.zhimg.com/v2-5d36f49befdcfd1361aa92c53921521a_r.jpg"/> 无奇点的黎曼 xi 函数
该函数满足关系
<img src="https://pic4.zhimg.com/v2-ab46b4b3b37b90d672de6f36522e467b_b.jpg" data-caption="" data-size="normal" data-rawwidth="918" data-rawheight="214" class="origin_image zh-lightbox-thumb" width="918" data-original="https://pic4.zhimg.com/v2-ab46b4b3b37b90d672de6f36522e467b_r.jpg"/> 黎曼 xi 函数正负值之间的对称关系
这意味着该函数关于垂线 Re(s) = 1/2 对称,使得 ξ(1) = ξ(0)、ξ(2) = ξ(-1) 等等。
此函数关系(s 与 1-s 的对称性)与欧拉乘积公式一同显示了黎曼 xi 函数 ξ(s) 只在区间 0 ≤ Re(s) ≤ 1 内有零点。换句话说,黎曼 xi 函数的零点对应于黎曼 zeta 函数的零点。在某种意义上,黎曼 zeta 函数的临界线 R(s) = 1/2 对应于黎曼 xi 函数 ξ(s) 的实数线(Im(s) = 0)。
任何人只要一看上面这两张图表,立刻就能注意到黎曼 zeta 函数 ζ(s) 的非平凡零点(即 黎曼 xi 函数的零点)的实部 Re(s) 都等于 1/2。黎曼在他的论文中简要地提到了这种现象,这一简短的注解,最终将成为他最伟大的遗产之一。
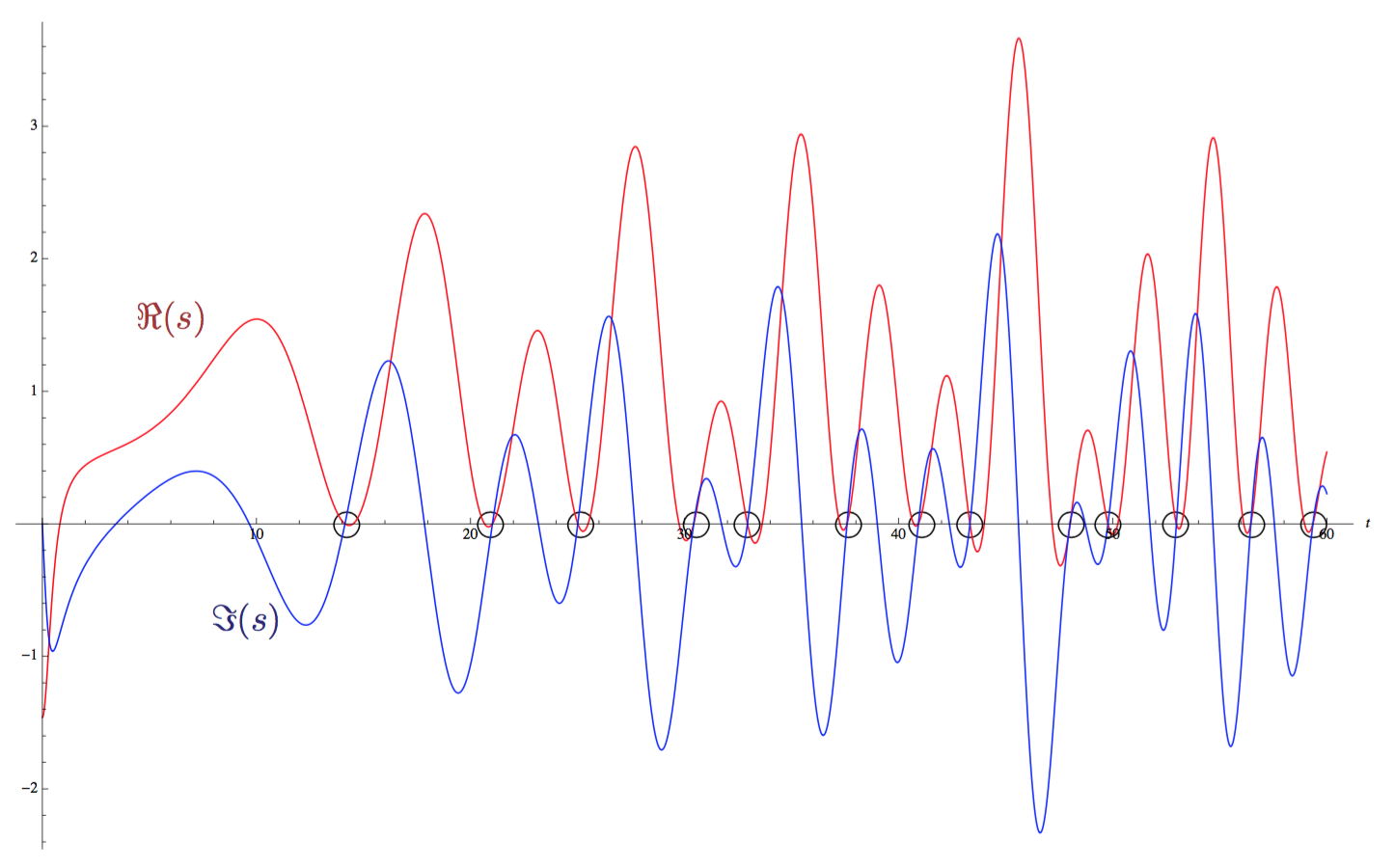
黎曼猜想 黎曼 zeta 函数 ζ(s) 非平凡零点的实部 Re(s) = 1/2。 这是黎曼在他著名的论文中提出的未证明的推测的现代表述。它指出 zeta 在临界带 0 ≤ Re(s) ≤ 1 中的零点,即 ζ(s) = 0,均有实部 Re(s) = 1/2。若果真如此,那么所有 zeta 的非平凡零点均有形式 ζ(1/2 + it)。一个等价的表述(黎曼的原始表述)为黎曼 xi 函数ξ(s) 的根均为实数。在下图中,直线 Re(s) = 1/2 为横轴。ζ(s) 的实部 Re(s) 图像为红色,而虚部 Im(s) 图像为蓝色。非平凡零点为红蓝图像在横轴上的交点。
<img src="https://pic2.zhimg.com/v2-3558a7b205809f73df973f610927e171_b.jpg" data-caption="" data-size="normal" data-rawwidth="1446" data-rawheight="900" class="origin_image zh-lightbox-thumb" width="1446" data-original="https://pic2.zhimg.com/v2-3558a7b205809f73df973f610927e171_r.jpg"/> 黎曼 zeta 函数在直线 Re(s) = 1/2 上的第一个非平凡零点
若黎曼猜想证明为真,则该函数的所有非平凡零点,即两图像的交点均会出现在该直线上。
相信黎曼猜想的理由 我们有很多理由相信黎曼关于 zeta 函数零点的猜想为真。对数学家而言,也许最吸引人的原因是它对于素数分布的意义。此猜想的数值验证到非常高的值时仍然为真。实际上,该猜想的数值证据已经足够强到在物理和化学这类领域中被视为经过实验验证了。然而,数学史上曾有几个推测,从数值上显示到非常高的值时为真,但仍然被证明是假的。德比夏尔(2004)讲述了斯奎斯数的故事,它给出了一个非常非常大的数值上界,否定了高斯的一个推测,即对数积分Li(x)总是大于素数计数函数。它被利特尔伍德不加反例地证否,然后表明它在非常非常大的斯奎斯数以上必定失效,该数为 10 的(10 的 (10 的 34 次方)次方)次方(10^(10^(10^34))),虽然高斯的猜想已经被证明有误,但要给出一个具体的例子仍远超现今的数值计算能力。对于黎曼猜想来说也是如此,它“只不过才”被验证了十的十二次方个非平凡零点而已。
黎曼 zeta 函数与素数 以黎曼猜想为真作为起点,黎曼开始研究其意义。他在论文中写道:“……很可能所有根都是实数。当然我们希望对此有一个严格的证明;经过一番短暂而徒劳的尝试后,我将它暂时搁置,因为它对我下的一个研究目标来说并不是必须的。”而他的下一个目标就是将 zeta 函数的零点与素数联系起来。回忆一下素数计数函数 π(x),它表示包括一个实数x以内的素数个数。黎曼用 π(x) 来定义他自己的素数计数函数,即黎曼素数计数函数 J(x)。它被定义为:
<img src="https://pic2.zhimg.com/v2-0c952d37345e9f57dacfc7152c362eb9_b.jpg" data-caption="" data-size="normal" data-rawwidth="1400" data-rawheight="171" class="origin_image zh-lightbox-thumb" width="1400" data-original="https://pic2.zhimg.com/v2-0c952d37345e9f57dacfc7152c362eb9_r.jpg"/> 黎曼素数计数函数
首先注意到该函数并非无限。对于某些项,该计数函数将为零,因为在 x < 2 时没有素数。以 J(100) 为例,该函数由七项构成,因为第八项对于 100 会包含一个根 8,它约等于 1.778279...,因此该素数计数函数项为零,而其和为 J(100) = 28.5333...。与素数计数函数一样,黎曼素数计数函数 J(x) 也是一个阶跃函数,它按照以下规则增加:
<img src="https://pic1.zhimg.com/v2-e4b90bc7dd14f44ae2d5de54dc6307a4_b.jpg" data-caption="" data-size="normal" data-rawwidth="1350" data-rawheight="268" class="origin_image zh-lightbox-thumb" width="1350" data-original="https://pic1.zhimg.com/v2-e4b90bc7dd14f44ae2d5de54dc6307a4_r.jpg"/> 黎曼素数计数函数可能的值
为了将 J(x) 的值与到包括 x 以内素数的个数联系起来,我们通过一个被称作莫比乌斯反演的过程(我不会在这展示它)恢复素数计数函数。其结果表达式为
<img src="https://pic2.zhimg.com/v2-6de9fcbf19056f4a32a6fa90118070f1_b.jpg" data-caption="" data-size="normal" data-rawwidth="776" data-rawheight="266" class="origin_image zh-lightbox-thumb" width="776" data-original="https://pic2.zhimg.com/v2-6de9fcbf19056f4a32a6fa90118070f1_r.jpg"/> 素数计数函数 π(x) 以及它与黎曼素数计数函数和莫比乌斯函数 μ(n) 的关系
还记得莫比乌斯函数可能的值为
<img src="https://pic2.zhimg.com/v2-75fb5f27051ef96cc26ef7c9c74420e1_b.jpg" data-caption="" data-size="normal" data-rawwidth="1054" data-rawheight="137" class="origin_image zh-lightbox-thumb" width="1054" data-original="https://pic2.zhimg.com/v2-75fb5f27051ef96cc26ef7c9c74420e1_r.jpg"/> 莫比乌斯函数 μ(n) 的三个可能的值
这意味着我们现在可以将素数计数函数写成一个关于黎曼素数计数函数的函数:
<img src="https://pic2.zhimg.com/v2-46f5079639283998b2f7d46f1f266c45_b.jpg" data-caption="" data-size="normal" data-rawwidth="1400" data-rawheight="114" class="origin_image zh-lightbox-thumb" width="1400" data-original="https://pic2.zhimg.com/v2-46f5079639283998b2f7d46f1f266c45_r.jpg"/> 素数计数函数写成关于黎曼素数计数函数的函数,对于前七个n值的图像
这个新的表达式仍然是个有限求和,因为当 x < 2 时 J(x) 为零,毕竟没有素数小于 2。若我们现在考察 J(100) 这个例子,会得到和式
<img src="https://pic4.zhimg.com/v2-a38787b2dfcbc19da6517030ff0d37bb_b.jpg" data-caption="" data-size="normal" data-rawwidth="1400" data-rawheight="264" class="origin_image zh-lightbox-thumb" width="1400" data-original="https://pic4.zhimg.com/v2-a38787b2dfcbc19da6517030ff0d37bb_r.jpg"/> 素数计数函数对于 x = 100
我们得到的就是 100 以内素数的个数。
欧拉乘积公式的变换 接下来,黎曼以欧拉乘积公式作为起点,推导出一种用微积分的微分语言来分析求解素数个数的方法。从欧拉乘积公式开始:
<img src="https://pic4.zhimg.com/v2-faad17485a4d12f394c81ddfd91df137_b.jpg" data-caption="" data-size="normal" data-rawwidth="1400" data-rawheight="138" class="origin_image zh-lightbox-thumb" width="1400" data-original="https://pic4.zhimg.com/v2-faad17485a4d12f394c81ddfd91df137_r.jpg"/> 欧拉乘积公式对于前五个素数的图像
首先两边取对数,然后重写括号中的分母,他推导出关系
<img src="https://pic2.zhimg.com/v2-adaba5d454847b296301276001800781_b.jpg" data-caption="" data-size="normal" data-rawwidth="1400" data-rawheight="136" class="origin_image zh-lightbox-thumb" width="1400" data-original="https://pic2.zhimg.com/v2-adaba5d454847b296301276001800781_r.jpg"/> 欧拉乘积公式的对数重写形式
然后,它用著名的麦克劳林-泰勒级数展开了右边的每一个对数项,创造出一个无限和的无限和,其中每一个无限和都对应于素数级数中的每一项。
<img src="https://pic2.zhimg.com/v2-367395e1f25c1e1c8acc07143b4363e5_b.jpg" data-caption="" data-size="normal" data-rawwidth="1400" data-rawheight="529" class="origin_image zh-lightbox-thumb" width="1400" data-original="https://pic2.zhimg.com/v2-367395e1f25c1e1c8acc07143b4363e5_r.jpg"/> 对数欧拉乘积公式前四项的泰勒展开
观察其中一项,如:
<img src="https://pic1.zhimg.com/v2-9e5b58cdf3abdb5aeb5332eb957168cc_b.jpg" data-caption="" data-size="normal" data-rawwidth="412" data-rawheight="270" class="content_image" width="412"/> 1/3^s 的麦克劳林展开的第二项
这一项,以及其它所有的项都可以用微积分表示成 J(x) 函数下区域的一部分。写成积分形式:
<img src="https://pic2.zhimg.com/v2-2e6911196d33a77b2ba4635fb34ff2a1_b.jpg" data-caption="" data-size="normal" data-rawwidth="1400" data-rawheight="274" class="origin_image zh-lightbox-thumb" width="1400" data-original="https://pic2.zhimg.com/v2-2e6911196d33a77b2ba4635fb34ff2a1_r.jpg"/> 1/3^s 的麦克劳林展开的第二项的积分形式
换句话说,通过欧拉乘积公式,黎曼展示了可以将离散的素数计数函数表示成连续的积分求和。我们的示例项在下图中展现为黎曼素数计数函数下区域的一部分。
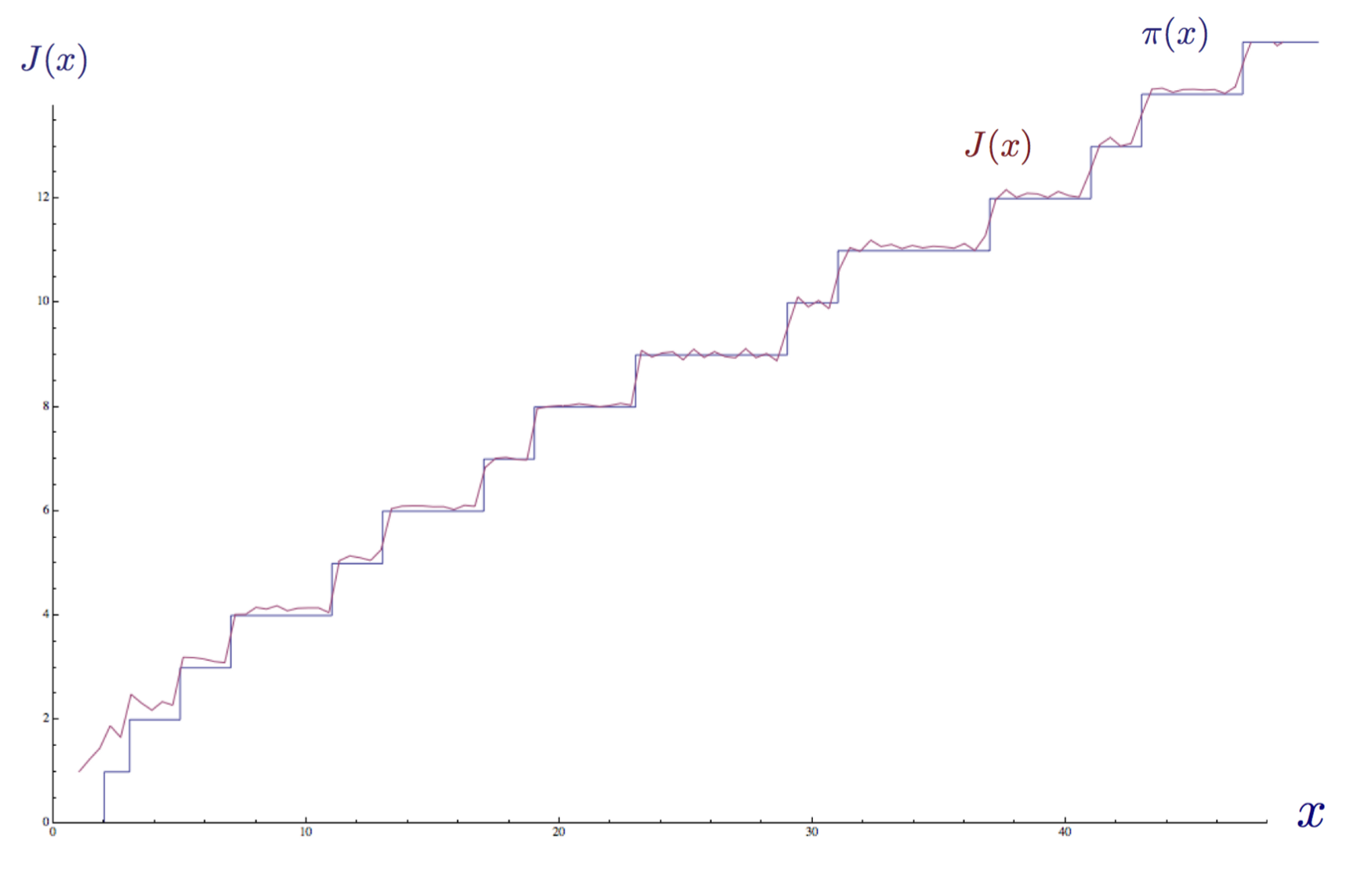
<img src="https://pic3.zhimg.com/v2-f15e318a83bb1d903755a6dd3eb5c2ce_b.jpg" data-caption="" data-size="normal" data-rawwidth="1750" data-rawheight="881" class="origin_image zh-lightbox-thumb" width="1750" data-original="https://pic3.zhimg.com/v2-f15e318a83bb1d903755a6dd3eb5c2ce_r.jpg"/> 黎曼素数计数函数 J(x) 绘制到 x = 50,两个积分已标出
因此,组成了欧拉乘积公式的素数倒数级数的无限积中的每个表达式都可以表示为积分,以此来创建对应于黎曼素计数函数下面积的积分的无穷和。对于素数 3,这个积分的无限积为:
<img src="https://pic3.zhimg.com/v2-3fd01e8e6eb8a13f5df62a7547651406_b.jpg" data-caption="" data-size="normal" data-rawwidth="1750" data-rawheight="159" class="origin_image zh-lightbox-thumb" width="1750" data-original="https://pic3.zhimg.com/v2-3fd01e8e6eb8a13f5df62a7547651406_r.jpg"/>
由整数 3 表示的素数计数函数下构成的区域积分的无穷积
将所有这些无穷和集成一个积分,那么黎曼素数计数函数 J(x) 下的积分可以简写为:
<img src="https://pic4.zhimg.com/v2-154dd910283dacc0cc1b3c3cfd704fb7_b.jpg" data-caption="" data-size="normal" data-rawwidth="1052" data-rawheight="214" class="origin_image zh-lightbox-thumb" width="1052" data-original="https://pic4.zhimg.com/v2-154dd910283dacc0cc1b3c3cfd704fb7_r.jpg"/>
zeta 的对数,表示为积分的无穷级数
或者,更受欢迎的形式:
<img src="https://pic1.zhimg.com/v2-f76acde661f64d3e6b7346b4b39032a4_b.jpg" data-caption="" data-size="normal" data-rawwidth="892" data-rawheight="194" class="origin_image zh-lightbox-thumb" width="892" data-original="https://pic1.zhimg.com/v2-f76acde661f64d3e6b7346b4b39032a4_r.jpg"/> 现代等价的欧拉乘积公式,将 zeta 函数与黎曼素数计数函数联系起来
黎曼用微积分的语言,通过这种方法将他的 zeta 函数 ζ(s) 与他的黎曼素数计数函数 J(x) 连接在一个等价于欧拉乘积公式的恒等式中。
误差项 在他得到欧拉乘积公式的分析版本后,黎曼接下来继续创造他自己的素数定理。他给出的明确形式是:
<img src="https://pic1.zhimg.com/v2-d34622becb20bad2fd8512014d70a0dc_b.jpg" data-caption="" data-size="normal" data-rawwidth="1400" data-rawheight="203" class="origin_image zh-lightbox-thumb" width="1400" data-original="https://pic1.zhimg.com/v2-d34622becb20bad2fd8512014d70a0dc_r.jpg"/> “黎曼素数定理”猜测的在一给定数量 x 以内的素数个数
这就是黎曼的明确公式。它是对素数定理的改进,能更准确地估计数字 x 及以内存在多少个素数。该公式有四个项:
第一项,或“主项”为对数积分 Li(x),它是根据素数定理对素数计数函数 π(x) 更好的估计。它是目前为止最大的项,并且像我们之前看到的那样,它高估了多少包含给定值x以内的素数个数。 第二项,或“周期项”为 x 的 ρ 次幂对 ρ 的对数积分求和(原图误为 p,感谢 第三项为常量 -log(2) = -0.6993147... 第四项,即最后一项是在 x < 2 上为零的积分,因为没有素数小于 2。当该积分约等于0.1400101... 时,它在2处有最大值 。 当该函数的值增大时,后两项的贡献是无穷小的。大数的主要“贡献者”是对数积分与周期和。影响见下图:
<img src="https://pic1.zhimg.com/v2-c203c1816703496cdc3ab7e147737d40_b.jpg" data-caption="" data-size="normal" data-rawwidth="1750" data-rawheight="1122" class="origin_image zh-lightbox-thumb" width="1750" data-original="https://pic1.zhimg.com/v2-c203c1816703496cdc3ab7e147737d40_r.jpg"/> 通过黎曼素数计数函数 J(x) 的明确公式使用黎曼 zeta 函数的前 35 个非平凡零点 ρ 来近似素数计步函数 π(x)
在上图中,我们通过黎曼素数计数函数 J(x) 的明确公示近似了素数计数函数 π(x),并对 zeta 函数 ζ(s) 的前 35 个非平凡零点求和。我们看到周期项会导致该函数“谐振”并开始接近素数计数函数 π(x) 的形状。 以下为使用了更多非平凡零点的同一图像。
<img src="https://pic4.zhimg.com/v2-754f013eae5392ab9f6fe7aacba0bc57_b.jpg" data-caption="" data-size="normal" data-rawwidth="1750" data-rawheight="1108" class="origin_image zh-lightbox-thumb" width="1750" data-original="https://pic4.zhimg.com/v2-754f013eae5392ab9f6fe7aacba0bc57_r.jpg"/> 通过黎曼素数计数函数 J(x) 的明确公式用黎曼 zeta 函数的前 100 个非平凡零点 ρ 来近似素数计步函数 π(x)
使用黎曼的显式函数,可以将包括给定数值x以内的素数近似到非常高的精度。实际上,冯·柯赫在 1901 年证明,使用黎曼猜想的零点来校正对数积分函数,等价于素数定理中误差项的“最佳可能”边界。
“……这些零点就像电线杆,而黎曼 zeta 函数的特殊性质严格决定了电线必须串连在它们之间……” 结语 自 1866 年黎曼 39 岁去世以来,他的突破性论文已经成为素数和分析数论领域的里程碑。到目前为止,尽管伟大的数学家们进行了数百年广泛的研究,然而关于黎曼 zeta 函数非平凡零点的黎曼猜想仍未解决。每年都会出版与此猜想有关的许多新的结果和猜想,希望有一天它能够确实地得到证明。
本文是 Jørgen Veisdal 2013 年本科毕业论文的重写。论文中引用了很多参考文献,我对此深表感谢,完整论文可从此处 下载。
对于有兴趣进一步探索本主题的人,我特别推荐 John Derbyshire 的 ‘Prime Obsession’ 一书。
译注 译者本人非数学专业,英语刚蹭过四级,所以文中大概存在相当多的翻译和理解问题。若有发现此类问题,恳请斧正。(咱不翻译文章,只是Google翻译+词典的搬运工= =||)
本文已征得原作者 Jørgen Veisdal 翻译授权,译文采用 CC-BY-SA 4.0 方式共享。
题图来自 Visualizing the Riemann zeta function and analytic continuation ,一个非常棒的视频,它以动画的方式讲解了黎曼 zeta 函数及其解析延拓,强烈推荐!(另有官方中英双语版 )
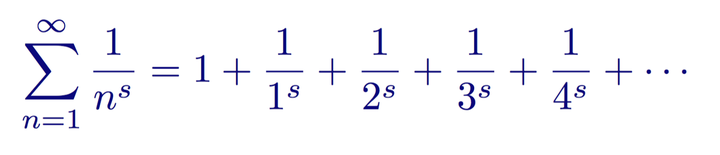
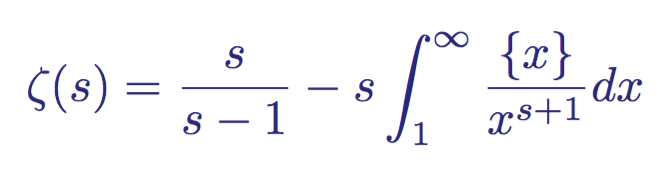






























89 条评论
number number;
showing that even though Gauss’ idea had been proven to be wrong, an example of exactly where is far beyond the reach of numerical calculation even today.
应该是 虽然Gauss的猜想已经被证明有误,但要给出一个具体的例子仍远超现今的数值计算能力。
综述形式的论文。毕竟本科生写一篇有实质性东西的论文很难,尤其是这种偏理论的数学科目,还有理论物理。写综述的人不少,就算是一个学习过程,把某一方面的内容做个总结。
我也是呀。。。不懂这里到底咋就是 undefined 。。。 回去查了一下原文,发现原文也没啥解释
这么简单的话,国家也不会花那么多钱去破译密码了
你想到的,人家早想到了
已验证了前10万亿个素数了