关于反三角函数及其导数

反三角函数是基本初等函数的重要组成部分，但似乎又是许多人常问的主体之一。为了方便理解和查询，本文总结了以下内容：

• 常见的六种三角函数对应的反三角函数的定义、定义域、值域，并给出对应三角形图示汇总、对应图象汇总
• 利用反函数求导法则完成了上述所有反三角函数的导数公式的推导，并详细总结了其值域、定义域等内容

本文内容也可作为备忘资料以便查阅使用。

一、常用三角函数与反三角函数

• 常见的六种三角函数可以分别由以下六种三角形表示

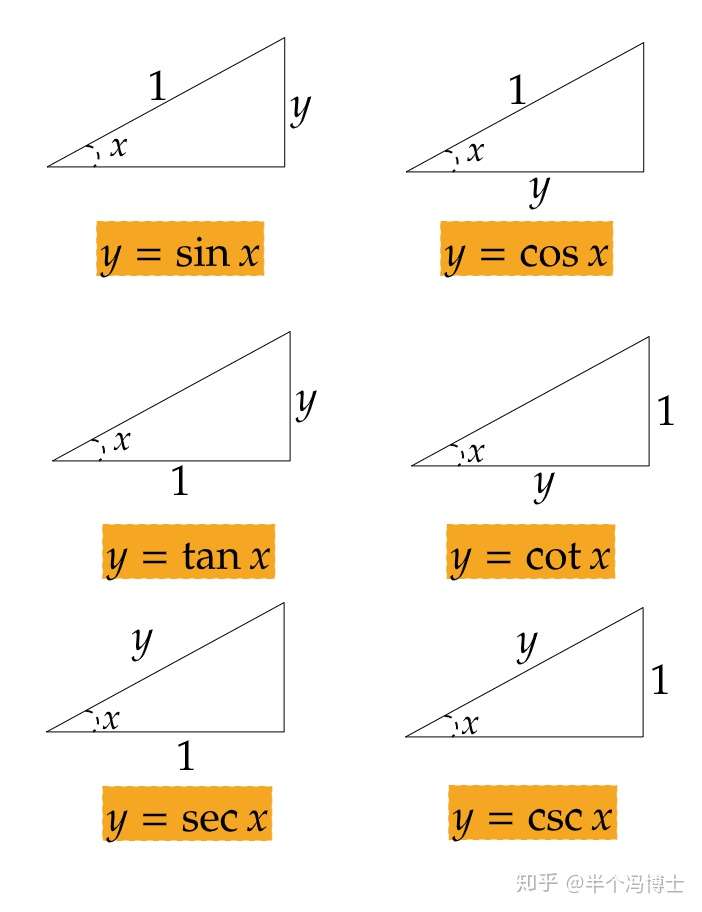
图1.三角函数及其对应三角形
​

• 反三角函数是三角函数的反函数。若将上图中所有x,y​ 调换位置则得到反三角函数的图示：

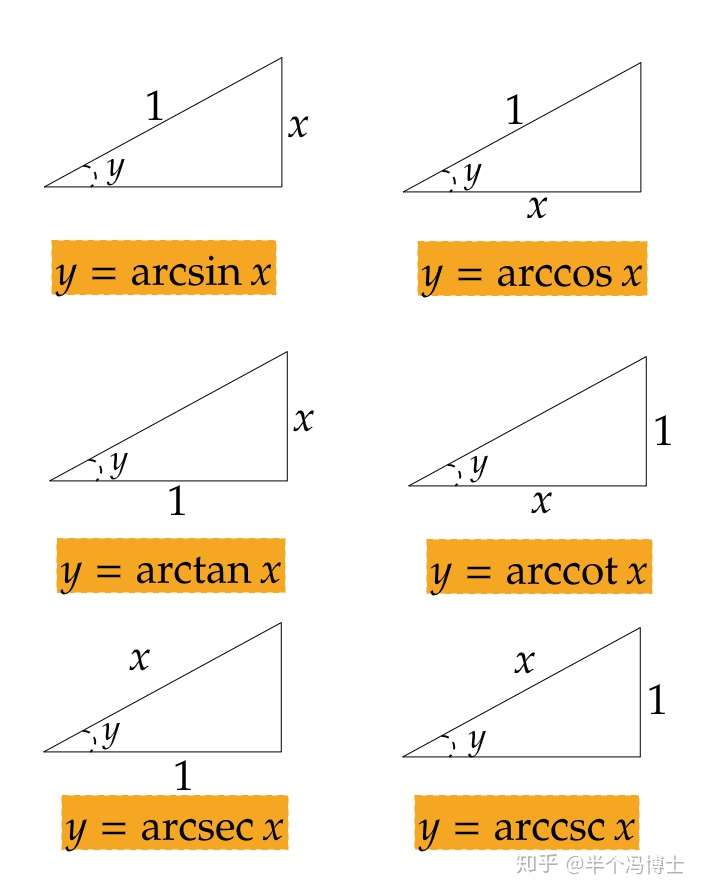
图2.反三角函数及其对应三角形

上述反三角函数的图象如下图所示：

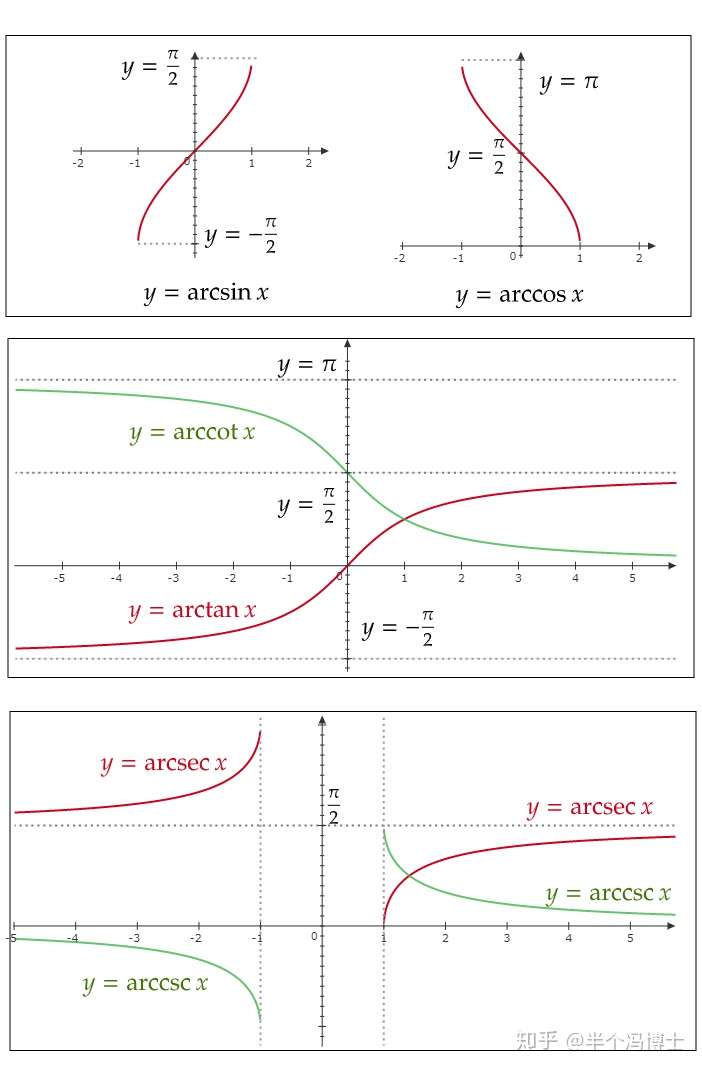
图3.反三角函数的图象

在使用反三角函数时一定要注意其定义值和值域。

表1. 反三角函数的定义值及值域 $\begin{array}{|c|c|c|c|} \hline \text { 反三角函数 } & \text { 三角函数} & \text {定义域} & 值域 \\ \hline y=\arcsin (x) & x=\sin (y) & -1 \leq x \leq 1 & -\frac{\pi}{2} \leq y \leq \frac{\pi}{2} \\ \hline y=\arccos (x) & x=\cos (y) & -1 \leq x \leq 1 & 0 \leq y \leq \pi \\ \hline y=\arctan (x) & x=\tan (y) & -\infty \le x +\infty & -\frac{\pi}{2}<y<\frac{\pi}{2} \\ \hline y=\operatorname{arccot}(x) & x=\cot (y) & -\infty \le x +\infty & 0<y<\pi \\ \hline y=\operatorname{arcsec}(x) & x=\sec (y) & x \leq-1 \text { or } 1 \leq x & 0 \leq y<\frac{\pi}{2} \text { or } \frac{\pi}{2}<y \leq \pi \\ \hline y=\operatorname{arccsc}(x) & x=\csc (y) & x \leq-1 \text { or } 1 \leq x & -\frac{\pi}{2} \leq y<0 \text { or } 0<y \leq \frac{\pi}{2} \\ \hline \end{array}$\begin{array}{|c|c|c|c|} \hline \text { 反三角函数 } & \text { 三角函数} & \text {定义域} & 值域 \\ \hline y=\arcsin (x) & x=\sin (y) & -1 \leq x \leq 1 & -\frac{\pi}{2} \leq y \leq \frac{\pi}{2} \\ \hline y=\arccos (x) & x=\cos (y) & -1 \leq x \leq 1 & 0 \leq y \leq \pi \\ \hline y=\arctan (x) & x=\tan (y) & -\infty \le x +\infty & -\frac{\pi}{2}<y<\frac{\pi}{2} \\ \hline y=\operatorname{arccot}(x) & x=\cot (y) & -\infty \le x +\infty & 0<y<\pi \\ \hline y=\operatorname{arcsec}(x) & x=\sec (y) & x \leq-1 \text { or } 1 \leq x & 0 \leq y<\frac{\pi}{2} \text { or } \frac{\pi}{2}<y \leq \pi \\ \hline y=\operatorname{arccsc}(x) & x=\csc (y) & x \leq-1 \text { or } 1 \leq x & -\frac{\pi}{2} \leq y<0 \text { or } 0<y \leq \frac{\pi}{2} \\ \hline \end{array}

二、反三角函数的导数的推导过程

反函数求导公式在另一篇笔记里已经回顾过：关于反函数的高阶导数

反函数的导 $(d\check{a} o)$(d\check{a} o) 数等于直接函数的导数的倒$(d \grave{a} o)$(d \grave{a} o) 数。

$$\frac{dx}{dy}=\frac{1}{\frac{dy}{dx}} \\$$ \frac{dx}{dy}=\frac{1}{\frac{dy}{dx}} \\

先给结论：

表2. 反三角函数的导数及其定义域

$\begin{array}{|l|c|c|} \hline 编号 &\text { 导数 } & \text { 定义域 } \\ \hline 1 &(\arcsin x)^{\prime}=\frac{1}{\sqrt{1-x^{2}}} & -1<x<1 \\ \hline 2 &(\arccos x)^{\prime}=-\frac{1}{\sqrt{1-x^{2}}} & -1<x<1 \\ \hline 3 &(\arctan x)^{\prime}=\frac{1}{1+x^{2}} & -\infty<x<\infty \\ \hline 4 &(\operatorname{arccot} x)^{\prime}=-\frac{1}{1+x^{2}} & -\infty<x<\infty \\ \hline 5 &(\operatorname{arcsec} x)^{\prime}=\frac{1}{|x| \sqrt{x^{2}-1}} & x \in(-\infty,-1) \cup(1, \infty) \\ \hline 6 &(\operatorname{arccsc} x)^{\prime}=-\frac{1}{|x| \sqrt{x^{2}-1}}& x \in(-\infty,-1) \cup(1, \infty) \\ \hline \end{array}$\begin{array}{|l|c|c|} \hline 编号 &\text { 导数 } & \text { 定义域 } \\ \hline 1 &(\arcsin x)^{\prime}=\frac{1}{\sqrt{1-x^{2}}} & -1<x<1 \\ \hline 2 &(\arccos x)^{\prime}=-\frac{1}{\sqrt{1-x^{2}}} & -1<x<1 \\ \hline 3 &(\arctan x)^{\prime}=\frac{1}{1+x^{2}} & -\infty<x<\infty \\ \hline 4 &(\operatorname{arccot} x)^{\prime}=-\frac{1}{1+x^{2}} & -\infty<x<\infty \\ \hline 5 &(\operatorname{arcsec} x)^{\prime}=\frac{1}{|x| \sqrt{x^{2}-1}} & x \in(-\infty,-1) \cup(1, \infty) \\ \hline 6 &(\operatorname{arccsc} x)^{\prime}=-\frac{1}{|x| \sqrt{x^{2}-1}}& x \in(-\infty,-1) \cup(1, \infty) \\ \hline \end{array}

接下来依次证明：

1、反正弦函数$y=\arcsin(x)$y=\arcsin(x)的导数

$$\begin{align*} \left( \arcsin x \right)^\prime &= \frac{1}{{{\left( \sin y \right)^\prime }}} &&\color{Red}{(\frac{dx}{dy}=\frac{1}{\frac{dy}{dx}})} \\ & = \frac{1}{\cos y} && \color{Red}{(\cos y\ge0)}\\ &= \frac{1}{{\sqrt{1 – \sin^2 y} }} &&\color{Red}{(y=\arcsin(x))} \\ &= \frac{1}{{\sqrt{1 – {\sin^2}\left( {\arcsin x} \right)} }} &&\color{Red}{(\sin \left ( {\arcsin x} \right ) =x )} \\ &= \frac{1}{{\sqrt{1 – {x^2}}}} \end{align*} \\$$ \begin{align*} \left( \arcsin x \right)^\prime &= \frac{1}{{{\left( \sin y \right)^\prime }}} &&\color{Red}{(\frac{dx}{dy}=\frac{1}{\frac{dy}{dx}})} \\ & = \frac{1}{\cos y} && \color{Red}{(\cos y\ge0)}\\ &= \frac{1}{{\sqrt{1 – \sin^2 y} }} &&\color{Red}{(y=\arcsin(x))} \\ &= \frac{1}{{\sqrt{1 – {\sin^2}\left( {\arcsin x} \right)} }} &&\color{Red}{(\sin \left ( {\arcsin x} \right ) =x )} \\ &= \frac{1}{{\sqrt{1 – {x^2}}}} \end{align*} \\

2、反余弦函数 $y=\arccos(x)$y=\arccos(x) 的导数

证法I： 类似推导

$$\begin{align*} \left( \arccos x \right)^\prime &= \frac{1}{{{\left( \cos y \right)^\prime }}} &&\color{Red}{(\frac{dx}{dy}=\frac{1}{\frac{dy}{dx}})} \\ & = -\frac{1}{\sin y} && \color{Red}{(\sin y\ge0)}\\ &= -\frac{1}{{\sqrt{1 – \cos^2 y} }} &&\color{Red}{(y=\arccos(x))} \\ &= -\frac{1}{{\sqrt{1 – {\cos^2}\left( {\arccos x} \right)} }} &&\color{Red}{(\cos\left ( {\arccos x} \right ) =x )} \\ &= \color{Blue}{- \frac{1}{{\sqrt{1 – {x^2}}}}} \end{align*} \\$$ \begin{align*} \left( \arccos x \right)^\prime &= \frac{1}{{{\left( \cos y \right)^\prime }}} &&\color{Red}{(\frac{dx}{dy}=\frac{1}{\frac{dy}{dx}})} \\ & = -\frac{1}{\sin y} && \color{Red}{(\sin y\ge0)}\\ &= -\frac{1}{{\sqrt{1 – \cos^2 y} }} &&\color{Red}{(y=\arccos(x))} \\ &= -\frac{1}{{\sqrt{1 – {\cos^2}\left( {\arccos x} \right)} }} &&\color{Red}{(\cos\left ( {\arccos x} \right ) =x )} \\ &= \color{Blue}{- \frac{1}{{\sqrt{1 – {x^2}}}}} \end{align*} \\

证法II：由$\arccos x =\frac{\pi}{2}-\arcsin x$\arccos x =\frac{\pi}{2}-\arcsin x，于是

$$\left ( \arccos x \right )^\prime =\left ( \frac{\pi}{2}-\arcsin x \right ) ^\prime = - \left ( \arcsin x \right ) ^\prime =-\frac{1}{\sqrt{1-x^2}} \\$$ \left ( \arccos x \right )^\prime =\left ( \frac{\pi}{2}-\arcsin x \right ) ^\prime = - \left ( \arcsin x \right ) ^\prime =-\frac{1}{\sqrt{1-x^2}} \\

3、反正切函数 $y=\arctan(x)$y=\arctan(x) 的导数

$$\begin{align*} \left( \arctan x \right)^\prime &= \frac{1}{{{\left( \tan y \right)^\prime }}} &&\color{Red}{(\frac{dx}{dy}=\frac{1}{\frac{dy}{dx}})} \\ & = \frac{1}{\frac{1}{\cos ^{2} y}} && \color{Red}{(\left( \tan y \right)^\prime=\sec^2x=\frac{1}{\cos ^{2} y})}\\ &= \frac{1}{1+\tan^2 y} &&\color{Red}{(\frac{1}{\cos ^{2} y}=\frac{\cos ^{2} y+\sin^{2} y}{\cos ^{2} y}=1+\tan^2 y)} \\ &= \frac{1}{{{1 + {\tan^2}\left( {\arctan x} \right)} }} &&\color{Red}{(\tan\left ( {\arctan x} \right ) =x )} \\ &= \frac{1}{{{1 + x^2}}} \end{align*} \\$$ \begin{align*} \left( \arctan x \right)^\prime &= \frac{1}{{{\left( \tan y \right)^\prime }}} &&\color{Red}{(\frac{dx}{dy}=\frac{1}{\frac{dy}{dx}})} \\ & = \frac{1}{\frac{1}{\cos ^{2} y}} && \color{Red}{(\left( \tan y \right)^\prime=\sec^2x=\frac{1}{\cos ^{2} y})}\\ &= \frac{1}{1+\tan^2 y} &&\color{Red}{(\frac{1}{\cos ^{2} y}=\frac{\cos ^{2} y+\sin^{2} y}{\cos ^{2} y}=1+\tan^2 y)} \\ &= \frac{1}{{{1 + {\tan^2}\left( {\arctan x} \right)} }} &&\color{Red}{(\tan\left ( {\arctan x} \right ) =x )} \\ &= \frac{1}{{{1 + x^2}}} \end{align*} \\

4、反余切函数 $y=\operatorname{arccot} (x)$y=\operatorname{arccot} (x) 的导数

证法I：类似3，略。

证法II： 类似2，由$y=\operatorname{arccot} (x)=\frac{\pi}{2}-\arctan(x)$y=\operatorname{arccot} (x)=\frac{\pi}{2}-\arctan(x) ，于是

$$\left ( \operatorname{arccot} x \right )^\prime =\left ( \frac{\pi}{2}-\arctan x \right ) ^\prime = - \left ( \arctan x \right ) ^\prime =-\frac{1}{1+x^2} \\$$ \left ( \operatorname{arccot} x \right )^\prime =\left ( \frac{\pi}{2}-\arctan x \right ) ^\prime = - \left ( \arctan x \right ) ^\prime =-\frac{1}{1+x^2} \\

5、反正割函数 $y=\operatorname{arcsec} (x)$y=\operatorname{arcsec} (x) 的导数

$$\begin{align*} \left( \operatorname{arcsec} x \right)^\prime &= \frac{1}{{{\left( \sec y \right)^\prime }}} &&\color{Red}{(\frac{dx}{dy}=\frac{1}{\frac{dy}{dx}})} \\ & = \frac{1}{\tan y \cdot \sec y} && \color{Red}{(\left( \sec y \right)^\prime =\tan y \cdot \sec y)}\\ &= \frac{1}{|\sec y| \cdot \sqrt{\sec^2 y -1}} &&\color{Red}{(*)} \\ &= \frac{1}{|\sec \left ( {\operatorname{arcsec} x} \right ) |\cdot \sqrt{\sec^2 \left ( {\operatorname{arcsec} x} \right ) -1}} &&\color{Red}{(\sec \left ( {\operatorname{arcsec} x} \right ) =x )} \\ &= \frac{1}{|x| \sqrt{x^{2}-1}} \end{align*} \\$$ \begin{align*} \left( \operatorname{arcsec} x \right)^\prime &= \frac{1}{{{\left( \sec y \right)^\prime }}} &&\color{Red}{(\frac{dx}{dy}=\frac{1}{\frac{dy}{dx}})} \\ & = \frac{1}{\tan y \cdot \sec y} && \color{Red}{(\left( \sec y \right)^\prime =\tan y \cdot \sec y)}\\ &= \frac{1}{|\sec y| \cdot \sqrt{\sec^2 y -1}} &&\color{Red}{(*)} \\ &= \frac{1}{|\sec \left ( {\operatorname{arcsec} x} \right ) |\cdot \sqrt{\sec^2 \left ( {\operatorname{arcsec} x} \right ) -1}} &&\color{Red}{(\sec \left ( {\operatorname{arcsec} x} \right ) =x )} \\ &= \frac{1}{|x| \sqrt{x^{2}-1}} \end{align*} \\

标 $\color{Red}{(*)}$\color{Red}{(*)}部分主要是要把上一步完全由 $\sec y$\sec y 表示，由于有以下恒等关系
i) $\ \sec^2 y - 1 = \frac{1}{\cos^2 y}-1 =\frac{1-\cos^2 y}{\cos^2 y}=\frac{\sin^2 y}{\cos^2 y}=\tan^2 y$\ \sec^2 y - 1 = \frac{1}{\cos^2 y}-1 =\frac{1-\cos^2 y}{\cos^2 y}=\frac{\sin^2 y}{\cos^2 y}=\tan^2 y
因此: $\tan y=\pm\sqrt{\sec^2 y -1}$\tan y=\pm\sqrt{\sec^2 y -1}
ii) 这时必须注意到 $y$y 的取值范围 $\left(0 \leq y<\frac{\pi}{2} \text { or } \frac{\pi}{2}<y \leq \pi\right)$\left(0 \leq y<\frac{\pi}{2} \text { or } \frac{\pi}{2}<y \leq \pi\right) (见表1.）。而在这一步中不能取任何一个端点。同时注意到：
$0 \leq y<\frac{\pi}{2}$0 \leq y<\frac{\pi}{2} 时：$\tan y,\sec y$\tan y,\sec y 都大等于$0$0
$\frac{\pi}{2}<y \leq \pi$$\frac{\pi}{2}<y \leq \pi$ 时： $\tan y,\sec y$\tan y,\sec y 都小等于 $0$0
因此： $\tan y \cdot\sec y>0$\tan y \cdot\sec y>0
综上：标$\color{Red}{(*)}$\color{Red}{(*)} 步的写法可以保证这一不等关系始终成立。

6、反余割函数 $y=\operatorname{arccsc} (x)$y=\operatorname{arccsc} (x) 的导数

证法I：类似5，略。

证法II： 类似2，由$y=\operatorname{arccsc} x=\frac{\pi}{2}-\operatorname{arcsec} x$y=\operatorname{arccsc} x=\frac{\pi}{2}-\operatorname{arcsec} x ，于是

$$\left ( \operatorname{arccsc} x \right )^\prime =\left ( \frac{\pi}{2}-\operatorname{arcsec} x \right ) ^\prime = - \left ( \operatorname{arcsec} x \right ) ^\prime =-\frac{1}{|x| \sqrt{x^{2}-1}} \\$$ \left ( \operatorname{arccsc} x \right )^\prime =\left ( \frac{\pi}{2}-\operatorname{arcsec} x \right ) ^\prime = - \left ( \operatorname{arcsec} x \right ) ^\prime =-\frac{1}{|x| \sqrt{x^{2}-1}} \\小结

本文简单总结了反三角函数的定义、其对应的三角函数、其定义域、值域，其后利用反函数求导法则完成了所有反函数求导公式的推导证明。不难看出上述推导过程其实都并不复杂（除反正割、反余割函数外），若能熟练使用各种三角函数变换技巧则能轻松完成所有证明。在实际使用三角函数时，图1,图2给出的图示十分有用，尤其在考虑积分换元时。另外，在使用反三角函数时，一定要明确各个三角函数的定义域及值域，这一点在第5个证明中体现得较为明显。若忽视这些细节，则十分容易出错。