图形学笔记 -- Color and Perception(颜色和感知)
Light Field、Color and Perception(光场、颜色和感知)。根据 闫令琪 课程整理。
各种颜色空间是怎么推导来的?400 纳米到 700 纳米。
What is Color?
- Color is a phenomenon of human perception; it is not a universal property of light
-
Different wavelengths of light are not “colors”
- 颜色的物理基础(谱功率密度(SPD))
- 颜色的生物学基础(视杆细胞、视锥细胞(S、M、L))
- 同色异谱
- 颜色匹配(加色实验)
- 颜色空间(sRGB、CIE XYZ、HSV、CIELAB(互补色))
- 减色系统(CMYK)
无意中看了 颜色几何学,讲了每个颜色空间的历史由来,多年的疑问全部烟消云散。第一代色环居然是牛顿定义的。
多年前对 OpenGL 函数也费解,设计的非常奇怪,后来也是无意中看了显卡的整个发展历史,才恍然大悟。
CIE XYZ(1931):开始尝试以数学方式拟合人眼视觉感知。
Lab(1976):追求“感知上均匀”的颜色距离。
OKLab(2020s):在新时代以更好的感知线性化,适应现代数字设计需求。
颜色的 "几何学 "是什么?
色彩空间为什么那么空?色度系统、色度图、色域、伽马、白点…
颜色的物理基础(Physical Basis of Color)
实验—光的基本成分(The Fundamental Components of Light)
早期,牛顿做过一个实验,一束白光穿过一个棱镜,它会被分解成各个不同的颜色(彩虹的颜色)。不同的颜色可以合成其他的颜色,将所有的颜色合在一起又会形成白色
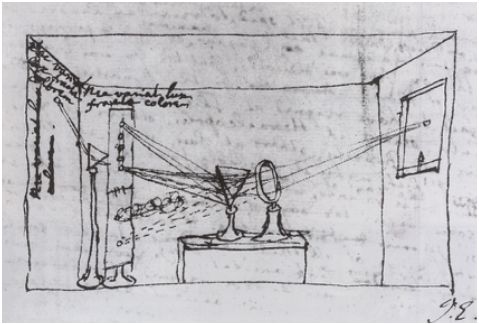
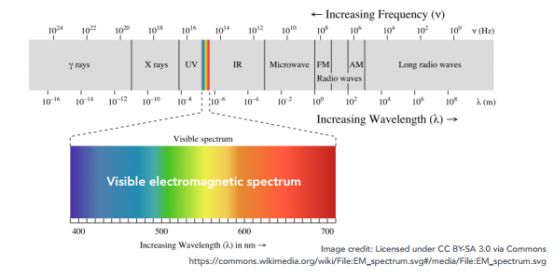
可见光谱(The Visible Spectrum of Light)
为什么光线会被折射成不同的颜色? 不同的波长对应不同的折射率,某一种光一定对应某一种 光谱( 光谱是光线的能量在不同的波长上的分布。光谱是一个很长的范围,但图形学中关心的是可见光的光谱,即分布在波长在 400nm 到 700nm 之间 )
谱功率密度(Spectral Power Distribution (SPD))
光谱 更准确的定义是 谱功率密度 (光线在不同的波长强度是多少)
单位 :辐射单位 / 纳米(例如瓦特 / nm),也可以是无单位的。
当绝对单位不重要时,通常使用缩放到最大波长的“相对单位”进行波长比较。
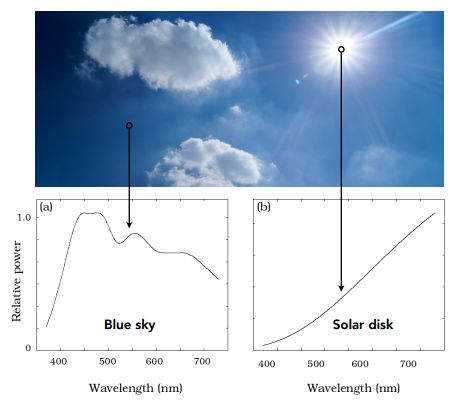
1)蓝天和日光的 SPD
如下图,可以看到图中某一个地方的能量是多少,对于蓝天部分,可以发现更多的能量集中在高频(小波长)的地方会看出蓝颜色;对于阳光,又是另外一种 SPD
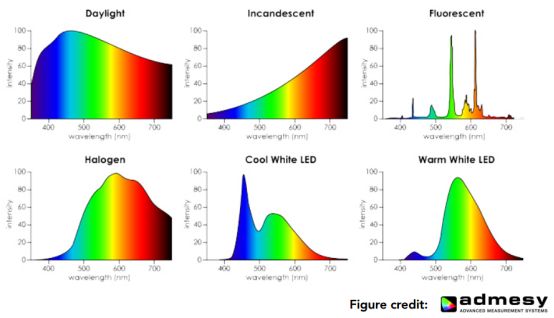
2)各种光源的 SPD
各种各样不同的光自然有各种不同的 SPD
3)SPD 的线性性质
如下图,比如有一个能记录光强度的东西,用某一种光照亮它,得到右边的某一种分布,另外一种光照亮它,得到另外一种分布;两种光同时照亮它,这个分布其实就是它们 2 个对应的 SPD 之和
可以想象开很多盏灯,会越来越亮
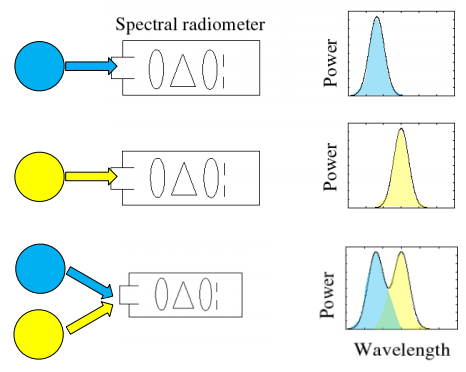
Brian Wandell
颜色的生物学基础(Biological Basis of Color)
什么是颜色? 我们最终要回答的问题是为什么能看到颜色,看到的是什么东西,而不是光谱。 颜色是人的感知(human perception) (和人有光,和实际光的分布其实并不一样)
人眼解剖结构(Anatomy of The Human Eye)
人的 眼睛 其实就是一个 摄像机: 人眼的 瞳孔 可调节大小,对应着 光圈 ; 晶状体 对应 透镜 ,可通过肌肉的拉扯调节焦距;视 网膜 进行成像
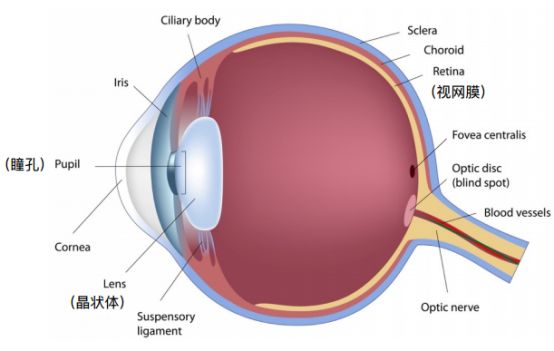
视网膜感光细胞(Retinal Photoreceptor Cells): Rods and Cones
视网膜是光线最终到达的地方,能看到东西是因为有感光细胞(如下图,视网膜内壁上有很多毛一样的东西),分为 2 种:
1)棒状细胞(视杆细胞)(Rod cells) :很多(~120 million),可以用来 感知光的强度,不感知颜色( 用这个棒状细胞 可以得到一个灰度的图)
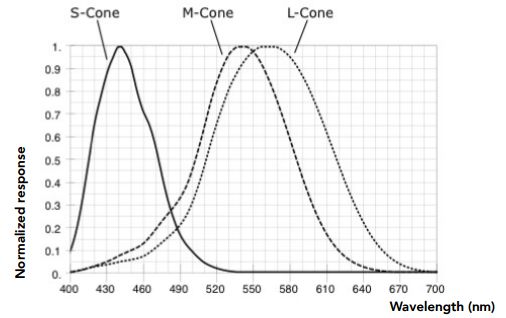
2)锥形细胞(视锥细胞)(Cone cells) :少很多(~6-7 million),可以用来 感知颜色 (为了研究颜色是怎么回事,应该去研究锥形的细胞)。 锥形细胞内部分成 S、M、L 这 3 种不同的锥形细胞(因为这三种细胞对三种类型的波长的响应各不相同)
- S 类型 :感知的是小波长(高频率)
- M 类型 :对中间波长的感知更灵敏
- L 类型 :感知的是长波长对应的光
下图是给不同的光,三种类型响应的曲线
三种细胞的分布和数量具有个体差异:
但不同的人以上这三种细胞的分布非常不一样,如下 12 幅图对应 12 个人眼睛里这三种视锥细胞的分布(分布很不一样,而且数量上有严重的个体差异)

颜色的三刺激理论(Tristimulus Theory of Color)
人们如何利用三种不同的细胞进行感知的?
我们定义了光在不同波长上的分布(SPD),又知道某一种细胞对于某一个波长的响应是多少。感知的函数就是这 2 个函数对应的位置相乘积分起来(相当于给你某一个波长,知道光线的强度是多少,将其和相应的感知的曲线的强度相乘,将每一个不同的波长都考虑进去)
三种不同的细胞自然会感应出三种颜色,对应下图的 S、M、L
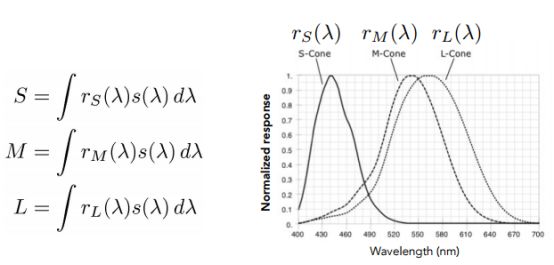
给定任何一种类型的光线(有任何的 SPD),人眼看到的是上面 S、M、L 这 3 个数,而不是光线本身的 SPD
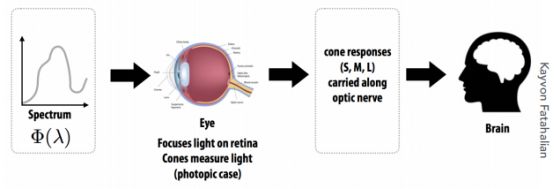
人的视觉系统(The Human Visual System)
光线的光谱经过人的眼睛,反应到视网膜上,然后被三种不同的细胞感知到形成 3 个数,这 3 个数送到人的脑袋中,人就会认为看到了一个什么样的颜色
同色异谱(Metamerism)
既然看到的不是光谱,而是光谱和各种各样的曲线积分出来的结果,那是有可能出现下面的现象的
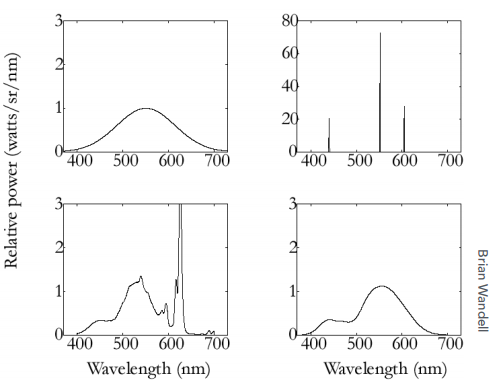
1)同色异谱现象 :2 种光线具有的光谱不相同,可是被我们看到的结果却是相同的
不同的信号进来后,通过积分得到 3 个数是相同的
2)颜色匹配(Color Matching): 利用这种现象给人们呈现各种不同的颜色,这个过程叫颜色匹配(通过调和不同的光谱,得到某一种颜色,使得这一种颜色和我看到的另外一种颜色一样。并不需要 2 个光的光谱一样,只需要最后的颜色一样)
下图是一些实际的光谱,它们的 SPD 完全不同,但被人感知之后(通过 3 个曲线积分之后),可以得到三个完全相同的结果
3)重要应用
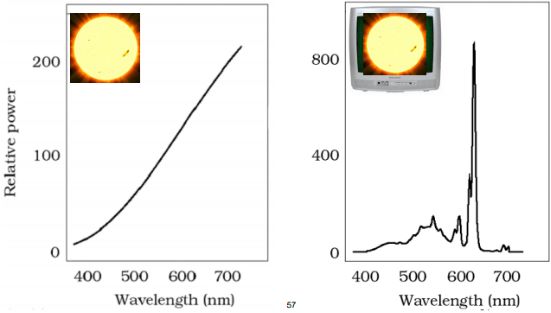
比如拍了太阳的一张照片,希望在显示器上可以显示出来,那么应该用什么样的颜色?
通过不同的调节方式,使得人看上去下面这 2 个颜色一样,但混合出来的光谱可以和之前的光谱长得完全不一样
Brian Wandell
Color Reproduction / Matching(颜色复制 / 匹配)
颜色应该如何混合?
计算机的成像系统是 加色系统(Additive) :有几种不同的原色(如下图,以最常见的 RGB 三种颜色为例),将各自不同的颜色乘上一个强度,将其混合起来,可以得到一种颜色,用它们各自混合的系数(强度)RGB 这 3 个数来表示颜色
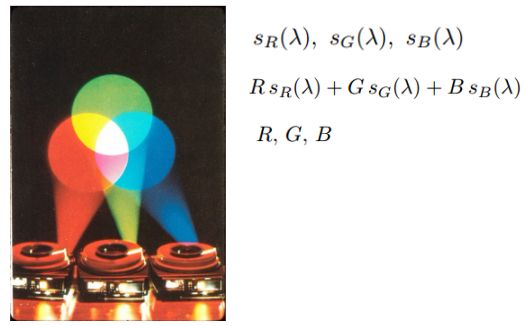
加色系统 :如果在计算机中将 RGB 的值都调到最高 255,得到白色。(在真实的世界里,不同的光照到同一个位置上,它们混合后会变强)
减色系统 :这个和画画不一样,如果调和不同的颜料,会越调越黑,就叫减色系统
Additive Color Matching Experiment(加色实验)
1)实验一
加色系统就可以使用上面的线性组合基本颜色的方式来匹配任何给定的颜色。如下图是一个基本的例子,给你任何一个颜色,希望用 3 种不同的颜色去混合匹配得到相同的额颜色
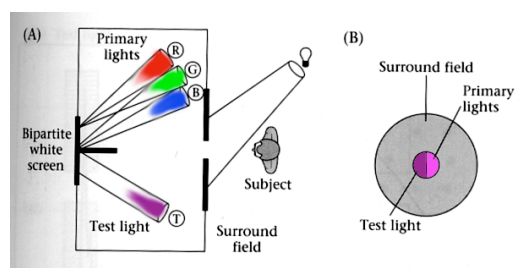
Slide courtesy of Prof. Ren Ng, UC Berkeley 左边是给定的颜色,右边是混合出的颜色,每一个颜色有一个系数(强度),将右边的颜色混合得和左边一样
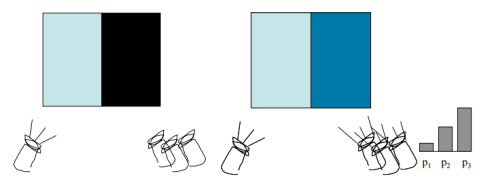
Slide from Durand and Freeman 06 也就是说找到了多强的 3 种颜色混合起来得到左边的颜色
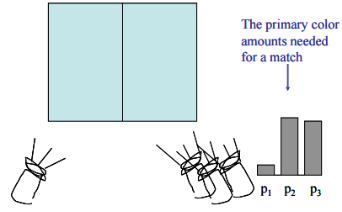
2)实验二
大多数情况可以通过上面的方法解决,但有时候对于左边的颜色右边无法混合出来
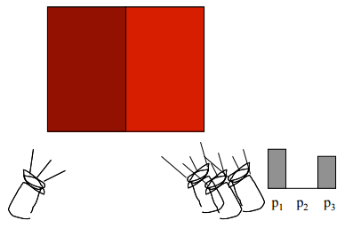
可以将左边给定的颜色往上加一个颜色(这就好像对应在右边减这个颜色,但因为用的加色系统无法减,最小是 0)
如果通过几种不同的颜色去混合得到一种颜色,这个不同的系数其实可能是负的
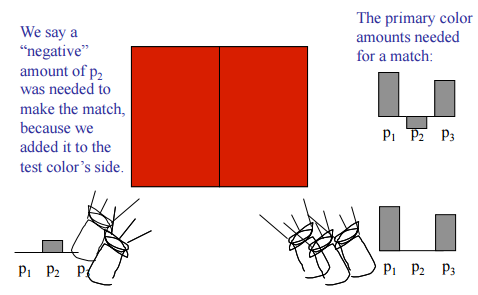
CIE RGB Color Matching Experiment(CIE RGB 配色实验)
从而发明了一个 CIE RGB 的系统,这就开始接近颜色空间的表示
CIE 是一个组织,它们定义了 RGB 的系统,这个系统要做颜色匹配,那给定的任何一个颜色是 单波长 的颜色(某种激光),光线的 SPD 是一个单一的Δ函数(或者理解成某一种曲线)。

要用 3 种同样是单色的光(在频谱上分布非常集中,如下图)
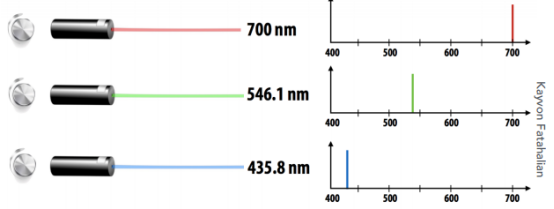
颜色匹配函数:
1)对于单波长的目标颜色
如下图,在做颜色的匹配,给你任何一个固定的波长,比如取 450,从图中我们可以看出波长为 450 时分别对应的蓝色、绿色、红色的值,如果要匹配出这个颜色就要将 3 个颜色使用对应的强度混合起来
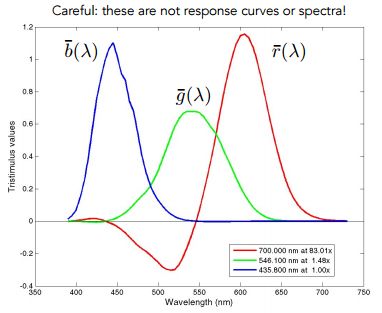
2)对于实际的光(多个波长)
上面匹配的是一个单色的光谱,如果给定一个实际光的光谱(SPD),就要使用积分考虑每一个波长所需要的红、绿、蓝,然后混合在一块
这 3 个颜色每一个积分出来会得到 3 个数
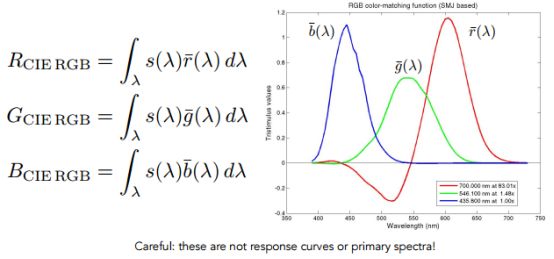
Color Spaces(颜色空间)
Standard Color Spaces:Standardized RGB (sRGB)
RGB 是广泛使用的一个标准的系统,它更准确名字应该叫 标准 RGB(或 sRGB)
sRGB 的颜色系统广泛的应用于各种成像设备(比如电脑显示器):先找某一台机器,这台机器的 RGB 做好后,后续的制造就按照这台机器的方法来制造
问题: RGB 颜色空间形成的 色域 是 有限 的
A Universal Color Space: CIE XYZ
虽然不常用,但在科学上应用得更为广泛
1)CIE XYZ 系统 也定义了一个 颜色匹配函数 (如下图),但这个颜色系统不是实验测出来的,而是人造的,先定义好以下的 3 种曲线(虚拟的):
- 可以看到 绿色 曲线的设计覆盖得比较全面,分布比较对称,所以绿色对应的 y 函数匹配出来的数 Y 在一定程度上可以表示颜色的 亮度
- 红色有 2 个峰值,没有负数,所有的这些函数都分布在可见光的范围内
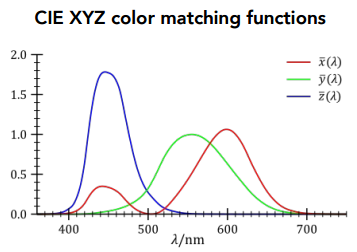
CIE XYZ 和 RGB 的区别就在匹配函数
2)将 x、y、z 能表示的颜色都显示出来
X、Y、Z 是三维的,如何在二维中进行可视化?
将 X、Y、Z 先进行 归一化 (这里使其加起来等于 1),得到 x、y、z
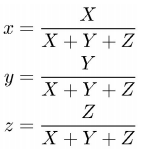
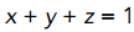
因为三个数加起来等于 1,那只 要显示前面 2 个维度 能得到一个什么样的图就可以了(为了显示前面 2 个维度,还是有 X、Y、Z 三个数的,而且既然知道 Y 表示的是亮度,那可以将其固定成某一个数,让 X、Z 发生变化,图中显示 x、y )
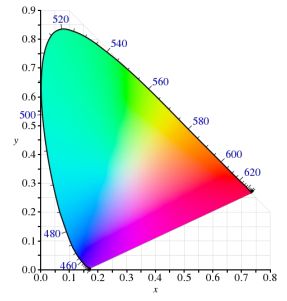
其实 改变大写的 Y ,也只是 改变它们的亮度
3)Gamut(色域)
可以看到上面的边界是扇形的,这个就是色域,整个颜色空间可以显示的颜色
如下图,这个色域有一个中心(白色,白色是由各种颜色混合起来的,所以白色是最不纯的颜色,纯的颜色都在边界上)
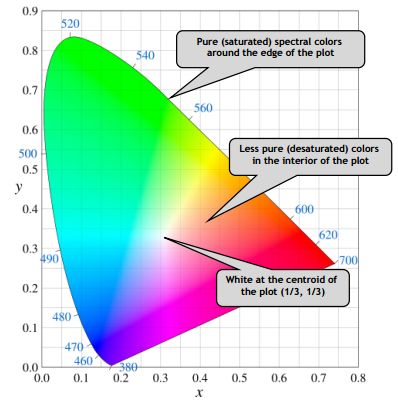
不同的颜色空间表示的颜色范围是不一样的
如下图,sRGB 只能表示下图很小的三角形部分的色域
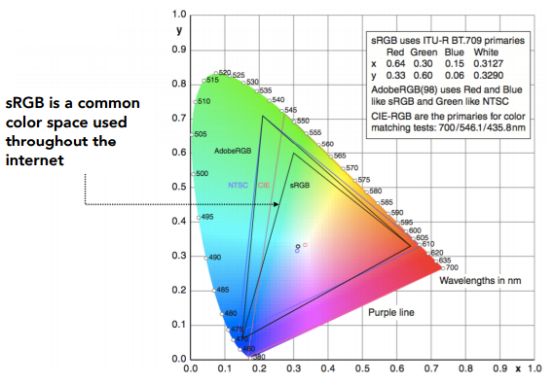
Perceptually Organized Color Spaces
1)HSV Color Space (Hue-Saturation-Value)
在 PS 中有用到,广泛应用于颜色拾取器
可以选择各种不同的色调(Hue)、饱和度(Saturation)、Brightness(亮度)/Value(值)
色调 :不同类型的颜色
饱和度 :更接近白色,还是更接近颜色本身的纯色
亮度: 从黑色一直到某种颜色
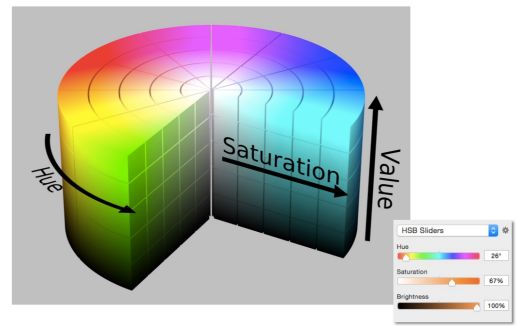
2)CIELAB Space (AKA L*a*b*)
LAB 色彩空间也和感知有关,如下图有 3 个:
L 轴 表示的是 亮度 (0 为黑,100 为白);
a 轴 上 红 和 绿 分别在两端;
b 轴 上 蓝 和 黄 在两端
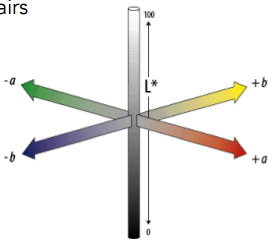
LAB 空间认为任何一个轴上两端都是 互补色 (比如可以理解成白色的反义词是黑色,它们两个就是互补色,像红色和绿色,蓝色和黄色互补是通过实验得到的)
Opponent Color Theory(互补色理论)
其实人的大脑对互补色是有一个定义的(比如我们可以想象有一个浅绿、深绿、黄绿、蓝绿,但不能想象一个偏红的绿色)
实验 1 :可以通过人眼的视觉暂留来验证互补色:
人眼的视觉暂留就是看一幅图看得时间长了,看到另外一幅图,你会看到第一幅图的互补色
当你盯着下面这幅图中的点看 10 秒左右,再看别的东西的一瞬间可以看到五星红旗

实验 2: 先看第一张图,之后会看到它的互补色,再看第二张灰度图,这样你会将互补色加到灰度图上,可以看到忍者神龟变绿

颜色很多都是相对的
颜色本身是感知,也就是说你看到的颜色有多强,是你觉得是这样,但和实际可能有相悖的效果
1)例子 1 :如下图,A 和 B 哪一个更亮,哪一个更暗?
你会觉得 B 比 A 亮
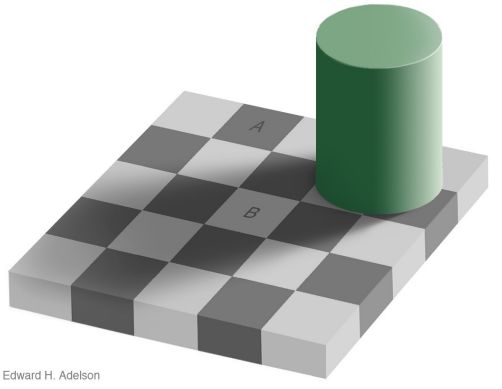
可是如果把除 A、B 之外的其他地方都挡住,你会发现 A 和 B 颜色是一样

2)例子 2 :下图黄色的叉,哪个更亮?
你会觉得左边的更亮

但如果在上面加上一个水平的纯色的条,你会发现 2 个颜色其实是完全一样的

减色系统 —— CMYK
减色系统在生活中应用得更加广泛(如打印、印刷)
给你不同的颜色,将其混合到一块,会越混越黑
CMYK :Cyan(蓝绿色)、Magenta(品红色)、Yellow(黄色)、Key(黑色)

如下图,C、M、Y 可以通过混合得到各种不同的颜色,所以在打印上,可以通过混合各种各样不同墨水调出各种各样不同的颜色
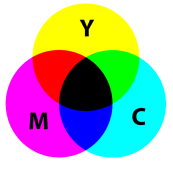
上图可以看到混合 C、M、Y 本来就可以得到黑色,那为什么还需要黑色?
因为在印刷上要考虑 成本 ,正常情况下打印东西以黑色居多,而且黑色的墨水好制作,便宜,C、M、Y 这三种带颜色的墨水不容易制作,那用这三种颜色混合得到黑色,成本就比直接用黑色高
参考资料快照
- 图形学笔记 -- Color and Perception(颜色和感知) | 02 Oct 2021
- 图形学笔记 -- 摄影入门 · 照相机与透镜,光圈、快门和景深 | 23 Sep 2021
- 图形学笔记 -- GAMES101: 现代计算机图形学入门(光线追踪和动画) | 01 Aug 2021
- 图形学笔记 -- GAMES101: 现代计算机图形学入门 | 11 Jul 2021
 .
.