NoteAI

编程与调试 -- 消失的除法，除法 duang 变乘法

Posted on December 2, 2022 (珠海)
C/C++  编程 

遇到一段代码，看不懂，研究了一下，无用的编程知识又增加了。

auto bytes = (char*)last - (char*)first;
auto count = (unsigned int)(-1227133513 * (bytes >> 3));

基本知识

整数溢出

note 关于整数的异常情况主要有三种：

  • 溢出 只有有符号数才会发生溢出。有符号数最高位表示符号，在两正或两负相加时， 有可能改变符号位的值，产生溢出。 溢出标志 OF 可检测有符号数的溢出。
  • 回绕 无符号数 0-1 时会变成最大的数，如 1 字节的无符号数会变为 255 ， 而 255+1 会变成最小数 0 。 进位标志 CF 可检测无符号数的回绕。
  • 截断 将一个较大宽度的数存入一个宽度小的操作数中，高位发生截断。

查资料

消失的除法指令：Part1

note

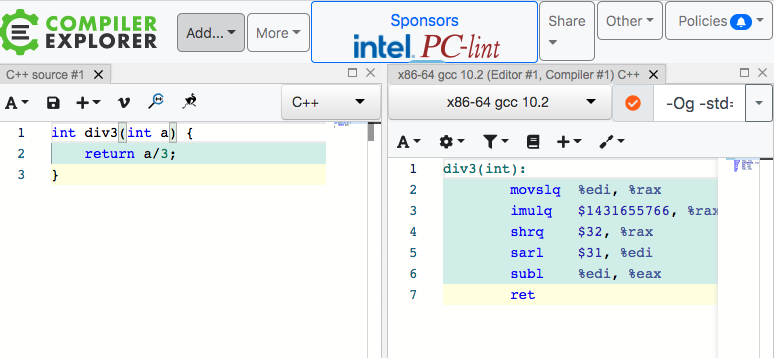
不管是浮点数还是整数，除法运算都比乘法运算要慢。 把除法变成乘法提高效率。

除法换成乘法 3435973837

note 在 gcc 里面有一个 32-bit 的 unsigned integer x，那么 x/10 会被转换成 (x*3435973837)>>35 。

for (int i = 0; i < 10; i++) {
    int a = i * 5;
    int b = a * 3435973837;
    printf("%u %u \n", a, b);
    assert(a / 5 == b);
}

除以 5 等价于 乘以 3435973837。 求一个 5 的倍数除 5 等于多少，可以换成乘法。

int main() {
    cout << 100 * 3435973837; // 输出 20
    return 0;
}

原理很简单： cout << 3435973837 * 5; 会输出 1，发生了溢出截断。

那么这个数是怎么来的呢？也很简单，解不定方程 $5x=2^{32}y+1$。 最小解是 $y=4, x=\frac{2^{34}+1}{5}=3435973837$。

除了 5 之外，其他所有奇数几乎都可以这么搞。

找代码

https://gmplib.org/devel/bc_bin_uiui.c Algorithm: Plain and simply multiply things together. We tabulate inverses ${(k/2^t)}^{-1}$ mod $B$ for $1=<k<=32$ (where $t$ is chosen such that $k/2^t$ is odd). 这里有一大批这样的数字，32 个。

https://datatracker.ietf.org/doc/html/draft-valin-celt-codec-00 "The CELT ultra-low delay audio codec", CELT website. celt-website is an open-source voice codec suitable for use in very low delay Voice over IP (VoIP) type applications. This document describes the encoding and decoding process. 这里有一大批这样的数字，128 个。

综合这些代码，我写了一个代码验证（32 位），居然全部通过了。

#include <iostream>
#include <assert.h>

static unsigned int zinvArray[] = {
    0x00000001,	/*  1 */  0x00000001,	/*  2 */
    0xaaaaaaab,	/*  3 */  0x00000001,	/*  4 */
    0xcccccccd,	/*  5 */  0xaaaaaaab,	/*  6 */
    0xb6db6db7,	/*  7 */  0x00000001,	/*  8 */
    0x38e38e39,	/*  9 */  0xcccccccd,	/* 10 */
    0xba2e8ba3,	/* 11 */  0xaaaaaaab,	/* 12 */
    0xc4ec4ec5,	/* 13 */  0xb6db6db7,	/* 14 */
    0xeeeeeeef,	/* 15 */  0x00000001,	/* 16 */
    0xf0f0f0f1,	/* 17 */  0x38e38e39,	/* 18 */
    0x286bca1b,	/* 19 */  0xcccccccd,	/* 20 */
    0x3cf3cf3d,	/* 21 */  0xba2e8ba3,	/* 22 */
    0xe9bd37a7,	/* 23 */  0xaaaaaaab,	/* 24 */
    0xc28f5c29,	/* 25 */  0xc4ec4ec5,	/* 26 */
    0x684bda13,	/* 27 */  0xb6db6db7,	/* 28 */
    0x4f72c235,	/* 29 */  0xeeeeeeef,	/* 30 */
    0xbdef7bdf,	/* 31 */  0x00000001	/* 32 */
};

static unsigned char ctzArray[] =
{ 0,1,0,2,0,1,0,3,0,1,0,2,0,1,0,4,0,1,0,2,0,1,0,3,0,1,0,2,0,1,0,5 };

void check(int num, int zinv, int ctz) {
    if (num <= 32) {
        printf("**[%d] %x,%d / ref %x,%d \n",
            num, zinv, ctz, zinvArray[num - 1], ctzArray[num - 1]);
        assert(zinv == zinvArray[num - 1]);
        assert(ctz == ctzArray[num - 1]);
    }
    for (int i = 0; i < 1000; i++) {
        if (i % num != 0) continue;
        auto value1 = i / num;
        auto value2 = zinv * (i >> ctz);
        // printf("%d,%d,%d,%d -- %d %d \n", i, num, zinv, ctz, value1, value2);
        assert(value1 == value2);
    }
}

/* INV_TABLE[i] holds the multiplicative inverse of (2*i+1) mod 2**32. */
static const unsigned int INV_TABLE[128] = {
    0x00000001, 0xAAAAAAAB, 0xCCCCCCCD, 0xB6DB6DB7,
    0x38E38E39, 0xBA2E8BA3, 0xC4EC4EC5, 0xEEEEEEEF,
    0xF0F0F0F1, 0x286BCA1B, 0x3CF3CF3D, 0xE9BD37A7,
    0xC28F5C29, 0x684BDA13, 0x4F72C235, 0xBDEF7BDF,
    0x3E0F83E1, 0x8AF8AF8B, 0x914C1BAD, 0x96F96F97,
    0xC18F9C19, 0x2FA0BE83, 0xA4FA4FA5, 0x677D46CF,
    0x1A1F58D1, 0xFAFAFAFB, 0x8C13521D, 0x586FB587,
    0xB823EE09, 0xA08AD8F3, 0xC10C9715, 0xBEFBEFBF,
    0xC0FC0FC1, 0x07A44C6B, 0xA33F128D, 0xE327A977,
    0xC7E3F1F9, 0x962FC963, 0x3F2B3885, 0x613716AF,
    0x781948B1, 0x2B2E43DB, 0xFCFCFCFD, 0x6FD0EB67,
    0xFA3F47E9, 0xD2FD2FD3, 0x3F4FD3F5, 0xD4E25B9F,
    0x5F02A3A1, 0xBF5A814B, 0x7C32B16D, 0xD3431B57,
    0xD8FD8FD9, 0x8D28AC43, 0xDA6C0965, 0xDB195E8F,
    0x0FDBC091, 0x61F2A4BB, 0xDCFDCFDD, 0x46FDD947,
    0x56BE69C9, 0xEB2FDEB3, 0x26E978D5, 0xEFDFBF7F,
    0x0FE03F81, 0xC9484E2B, 0xE133F84D, 0xE1A8C537,
    0x077975B9, 0x70586723, 0xCD29C245, 0xFAA11E6F,
    0x0FE3C071, 0x08B51D9B, 0x8CE2CABD, 0xBF937F27,
    0xA8FE53A9, 0x592FE593, 0x2C0685B5, 0x2EB11B5F,
    0xFCD1E361, 0x451AB30B, 0x72CFE72D, 0xDB35A717,
    0xFB74A399, 0xE80BFA03, 0x0D516325, 0x1BCB564F,
    0xE02E4851, 0xD962AE7B, 0x10F8ED9D, 0x95AEDD07,
    0xE9DC0589, 0xA18A4473, 0xEA53FA95, 0xEE936F3F,
    0x90948F41, 0xEAFEAFEB, 0x3D137E0D, 0xEF46C0F7,
    0x028C1979, 0x791064E3, 0xC04FEC05, 0xE115062F,
    0x32385831, 0x6E68575B, 0xA10D387D, 0x6FECF2E7,
    0x3FB47F69, 0xED4BFB53, 0x74FED775, 0xDB43BB1F,
    0x87654321, 0x9BA144CB, 0x478BBCED, 0xBFB912D7,
    0x1FDCD759, 0x14B2A7C3, 0xCB125CE5, 0x437B2E0F,
    0x10FEF011, 0xD2B3183B, 0x386CAB5D, 0xEF6AC0C7,
    0x0E64C149, 0x9A020A33, 0xE6B41C55, 0xFEFEFEFF
};

int main()
{
    int count = sizeof(zinvArray) / sizeof(zinvArray[0]);
    int count2 = sizeof(ctzArray) / sizeof(ctzArray[0]);
    assert(count == count2);
    for (int i = 0; i < count; i++) {
        check(i + 1, zinvArray[i], ctzArray[i]);
    }

    int countx = sizeof(INV_TABLE) / sizeof(INV_TABLE[0]);
    for (int num = 1; num <= 2000; num++) {
        if (num % 2 == 0) {
            int shift = 0;
            int temp = num;
            while (temp && (temp % 2 == 0)) {
                shift++;
                temp = temp >> 1;
            }
            int index = (temp - 1) / 2;
            if (index >= countx) continue;
            printf("num=%d idx=%d inv=%x shift=%d \n",
                num, index, INV_TABLE[index], shift);
            check(num, INV_TABLE[index], shift);
        }
        else {
            int index = (num - 1) / 2;
            if (index >= countx) continue;
            printf("num=%d idx=%d inv=%x shift=%d \n",
                num, index, INV_TABLE[index], 0);
            check(num, INV_TABLE[index], 0);
        }
    }

    getchar();
    return 0;
}

这玩意必须是奇数，不是奇数的通过逻辑右移处理成奇数，而且必须是整除的才可以，否则算出来的数字很多也是不对的。

更多资料

cwrs.c Math behind gcc9+ modulus optimizations

整数定数除法的代换 (constant integer division) Shift to divide by 10 

// 32bit examples for _Bool mod_n(unsigned x){return x%n==0;};
// note: parameter is unsigned but it becomes a signed multiply
x%3==0;  // x*0xAAAAAAAB <= 0x55555555
x%5==0;  // x*0xCCCCCCCD <= 0x33333333
x%7==0;  // x*0xB6DB6DB7 <= 0x24924924
x%11==0; // x*0xBA2E8BA3 <= 0x1745D174
x%13==0; // x*0xC4EC4EC5 <= 0x13B13B13
x%17==0; // x*0xF0F0F0F1 <= 0x0F0F0F0F
x%19==0; // x*0x286BCA1B <= 0x0D79435E
x%23==0; // x*0xE9BD37A7 <= 0x0B21642C
x%29==0; // x*0x4F72C235 <= 0x08D3DCB0
x%31==0; // x*0xBDEF7BDF <= 0x08421084
x%37==0; // x*0x914C1BAD <= 0x06EB3E45
x%41==0; // x*0xC18F9C19 <= 0x063E7063
x%43==0; // x*0x2FA0BE83 <= 0x05F417D0
x%47==0; // x*0x677D46CF <= 0x0572620A
x%53==0; // x*0x8C13521D <= 0x04D4873E
x%59==0; // x*0xA08AD8F3 <= 0x0456C797
x%61==0; // x*0xC10C9715 <= 0x04325C53
x%67==0; // x*0x07A44C6B <= 0x03D22635
x%71==0; // x*0xE327A977 <= 0x039B0AD1
x%73==0; // x*0xC7E3F1F9 <= 0x0381C0E0
x%79==0; // x*0x613716AF <= 0x033D91D2
x%83==0; // x*0x2B2E43DB <= 0x03159721
x%89==0; // x*0xFA3F47E9 <= 0x02E05C0B
x%97==0; // x*0x5F02A3A1 <= 0x02A3A0FD
// ...and even up to 64bit
x%4294967291==0; // x*0x70A3D70A33333333 <= 0x100000005

应用

这玩意有一个限制，必须能整除，才适用。 蚊子肉再少也是肉，意义并不是很大，只有在那种大规模运算的场景，才能体现价值，比如素数运算，实时视频。

判断 vector 成员个数。

这里用 std::vector<cv::Mat> 举例，因为这个场景下，必定能整除。

std::vector<cv::Mat> myvec;

标准的 std::vector 是三个成员指针，本别是 pfirst, plast, pend。 Debug 版本 sizeof(myvec) == 16，Release 版本 sizeof(myvec) == 12。 可以定义一个宏，取出这三个指针。

#if _ITERATOR_DEBUG_LEVEL != 0
#define MatVecFirst(myvec) (  (cv::Mat*)  ((size_t*)&(myvec))[1]  )
#define MatVecLast(myvec)  (  (cv::Mat*)  ((size_t*)&(myvec))[2]  )
#define MatVecEnd(myvec)   (  (cv::Mat*)  ((size_t*)&(myvec))[3]  )
#else
#define MatVecFirst(myvec) (  (cv::Mat*)  ((size_t*)&(myvec))[0]  )
#define MatVecLast(myvec)  (  (cv::Mat*)  ((size_t*)&(myvec))[1]  )
#define MatVecEnd(myvec)   (  (cv::Mat*)  ((size_t*)&(myvec))[2]  )
#endif

然后通过 last & fist 指针，得到长度 bytes。

#define MatVecLen(myvec)   ((char*)MatVecLast(myvec) - (char*)MatVecFirst(myvec))

而 sizeof(cv::Mat) 是 56，很显然，这个长度除以 56 就是 vector 里面的元素个数。 但是我们搞点奇淫技巧，不除，那个慢，我们用乘法实现。

#define MatVecCount(myvec) ((unsigned int)(-1227133513 * (MatVecLen(myvec) >> 3)))

右移 3，相当于 除以 8，然后乘以 -1227133513 相当于除以 7，最终效果就是 除以了 56，这也回答了开篇那个问题。 而 为了增强 64 位版本的程序可移植性 ，可以尝试强制 (unsigned int) 限制。

危险的 (unsigned int)(float) 强转

if (outx == 0) {
    auto xxd = v25 * 255.0;
    float xxdf = (float)xxd;
    int t1 = (int)xxdf;
    int t2 = (unsigned int)xxdf; // 这里 32 系统，64 系统不一样。
    printf("v25 = %f \n", v25);
    printf("v25 = %f \n", xxd);
    printf("v25 = %f %x  %x:%x \n", xxdf, *(_DWORD*)&xxdf, t1, t2);
    printf("v25 = %x %d \n", (unsigned int)xxdf, temp);
}

Windows 32 位：

v25 = -0.333500
v25 = -85.042499
v25 = -85.042496 c2aa15c2  ffffffab:ffffffff
v25 = ffffffff 255
// 生成的汇编不一样，造成计算误差。
movss       xmm0,dword ptr [ebp-0C8h]
call        __ftoui3 (0F1B1708h)
mov         dword ptr [ebp-0D0h],eax

Windows 64 位：

v25 = -0.333500
v25 = -85.042499
v25 = -85.042496 c2aa15c2  ffffffab:ffffffab
v25 = ffffffab 171
// 生成的汇编不一样，造成计算误差。
cvttss2si   rax,dword ptr [rsp+140h]
mov         dword ptr [rsp+148h],eax

C++ 数据类型

  • 主要就是指针和 int 的问题。
类型 Win32 Win64 Android32 Android64
char 1 1 1 1
short 2 2 2 2
int 4 4 4 4
long 4 4 4 8（巨坑）
long long 8 8 8 8
int64 8 8 8 8
float 4 4 4 4
double 8 8 8 8
long double 8 8 8 16
void* 4 8 4 8
size_t 4 8 4 8

note 补码最大好处就是不管是有符号数还是无符号数都可以用同一套加减法。 有符号数和无符号数在计算机里表示都是一样的，二进制的补码形式。 是有符号还是无符号，是编译器来辨认的。

  • 赋值截断问题
    • 等长直接赋值，变短直接截断，变长如果正前补 0，为负前补 1，浮点数同理。
    • char a = 0xf1; unsigned b = a; // 0xfffffff1
    • unsigned b = 0xffffff01; char a = (char)b; // 0x01
  • 运算问题
    • 汇编是不区分正负数字的。溢出不溢出，是由程序员判断的，机器不管。
      • 溢出标志 OF 可检测有符号数的溢出。
      • 进位标志 CF 可检测无符号数的回绕。
  • 判等问题
    • movsx eax, byte ptr [a] 先符号扩展，再传送
    • movzx ecx, byte ptr [b] 先零扩展，再传送
    • cmp eax, ecx
  1. 一般 singed 型数据和 unsigned 型数据进行四则运算，是要转换成 unsigned 的。
  2. 两种数据类型相乘，会将其转换成范围更广的数据类型，再作运算。 如 unsigned short 与 int 相乘，会被转成 int 再作相乘，其最终结果也被认为是有符号的。
  3. 不同符号数的混合计算，在计算之前需要先对操作数进行规整化的动作， 规整的原则就是如果操作数中存在至少一个无符号数（前提要求两个操作数据位长是一致的）， 则所有操作数都被转化为无符号数， 运算操作也采用相应的无符号操作符进行，计算完的结果也是一个无符号数。 note 
    (unsigned int)b / (signed int)a
// 会采用无符号除法进行，其实质相当于：
(unsigned int)b / (unsigned int)a
// 计算结果也是一个无符号数，结果为
(unsigned int)2 / (unsigned int)-1
    = 0x2/0xFFFFFFFF = 0
// 再进一步，对于运算 -2 / -1，
// 如果采用有符号数运算，结果是 2，
// 采用无符号数运算，结果则是 0。
  4. 浮点数（float，double）实际上都是有符号数，unsigned 和 signed 前缀不能加在 float 和 double 之上，当然就不存在有符号数根无符号数之间转化的问题了。

IEEE754 标准，该标准定义了 float 和 double，float 有 32 位，double 有 64 位，不管是 32 位还是 64 位，它们都由符号位，指数位，和尾数位构成：

种类 符号位 指数位 尾数位
float 第 31 位（占 1bit） 第 30~23 位（占 8bit） 第 20~0 位（占 23bit）
double 第 63 位（占 1bit） 第 62~52 位（占 11bit） 第 51~0 位（占 52bit）
原类型 目标类型 转换方法
char unsigned long 符号位扩展到 long；然后从 long 转换到 unsigned long
char float 符号位扩展到 long；然后从 long 转到 float
char double 符号位扩展到 long；然后从 long 转换到 double
unsigned char unsigned long 0 扩展
unsigned char float 转换到 long；然后从 long 转换到 float
unsigned char double 转换到 long；然后从 long 转换到 double

比 int 低级的类型，都会转换成 int，比 int 高级的类型不变。

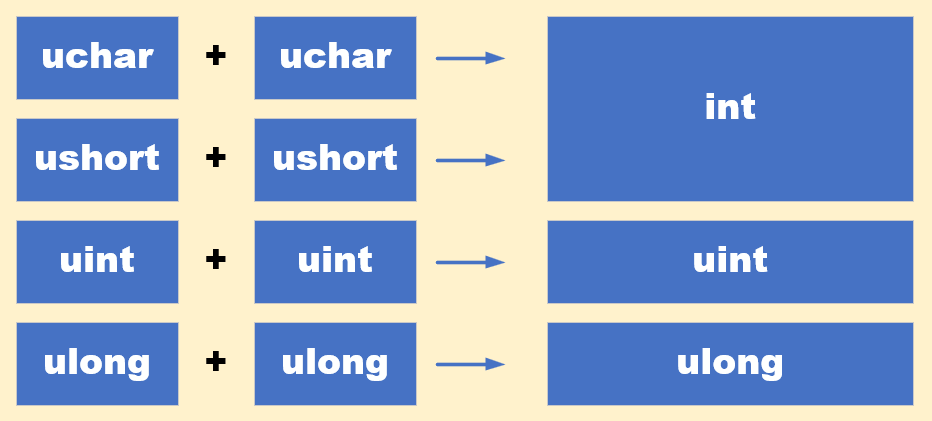
若运算符两边类型均低于 int 或等于 int，那么结果为 int。 若有高于 int 的，那么结果为高于 int 的等级最高的类型。

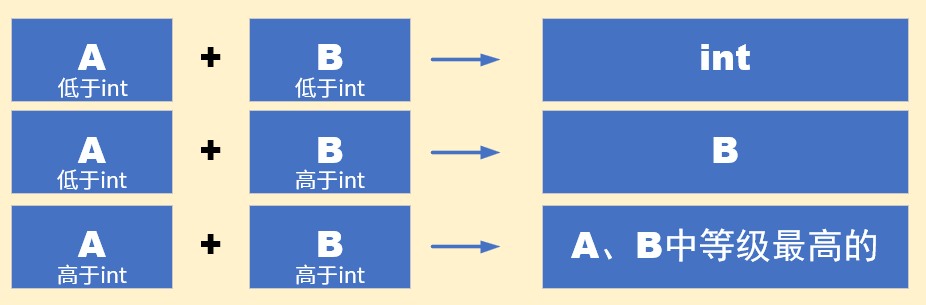
note int < unsigned int < long < unsigned long < float < double char，short，unsigned char，unsigned short 总是会被转换为 int。

参考资料快照
参考资料快照
本文短链接：
If you have any questions or feedback, please reach out .
自由转载-非商用-非衍生-保持署名
（创意共享 3.0 许可证）