MATHEMATICS --《线性代数》宋浩老师（已完成）

Posted on August 23, 2022 (珠海)
数学

外练筋骨皮，内练一口气，如果想要在互联网行业中生存下去，越来越需要高能力，高素质，已经不是以前的时代了。宋浩三部曲之二 ·《线性代数》。

《线性代数》
《微积分》
《概率论与数理统计》
《高等数学》

从新学习，并用 mathjax 做笔记。 mathjax html2text 公式及时编辑在线函数图像

image note

光线追踪 / 中山影视城

第一章行列式
第二章矩阵
第三章向量
第四章线性方程组
第五章特征值与特征向量
第六章二次型

先用考试逼着大家把该学的东西都学了，尽管自己也不知道自己学的是啥；等将来的某一天达到一定高度时，回头看看过去学的东西，突然恍然大悟，明白了当初学的究竟是什么。

这 4 部分数学知识的作用分别是：

概率统计是利用数据发现规律、推测未知的思想方法。
线性代数是利用空间投射和表征数据的基本工具。
微积分与最优化是机器学习模型中最终解决方案的落地手段。
概率图和随机过程是构成机器学习中的核心思想和大量核心应用。

1.1 二阶三阶行列式 38:52

完成。

行列式的真正定义：每个单位正方形在线性变换之后的面积。 因此，单位矩阵的行列式当然就为 1，某行全为 0 的行列式显然为 0 （因为某一维度会被无视掉，线性变换会把整个平面压扁）， $|A·B|$ 显然等于 $|A|·|B|$ 。行列式为 0 ，对应的矩阵当然不可逆，因为这样的线性变换已经把平面压成一条线了，什么都不能把它变回去了。当然，更高阶的矩阵就对应了更高维的空间。

1.1 n 阶行列式 43:55

完成。 note

比如三阶： $D = \begin{vmatrix} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \end{vmatrix}$

\[D = (-1)^{1+1}a_{11}\begin{vmatrix} a_{22}&a_{23} \\ a_{32}&a_{33} \end{vmatrix} + (-1)^{1+2}a_{12}\begin{vmatrix} a_{21}&a_{23} \\ a_{31}&a_{33} \end{vmatrix} + (-1)^{1+3}a_{13}\begin{vmatrix} a_{21}&a_{22} \\ a_{31}&a_{32} \end{vmatrix} \\ =a_{11}\begin{vmatrix} a_{22}&a_{23} \\ a_{32}&a_{33} \end{vmatrix} -a_{12}\begin{vmatrix} a_{21}&a_{23} \\ a_{31}&a_{33} \end{vmatrix} + a_{13}\begin{vmatrix} a_{21}&a_{22} \\ a_{31}&a_{32} \end{vmatrix} \\ = a_{11}a_{22}a_{33} -a_{11}a_{23}a_{32} - a_{12}a_{21}a_{33}+ a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} - a_{13}a_{22}a_{31}\]

1.2 行列式的性质 1:16:58

转置。

性质 1：$D^{\top}=D$ 对行成立的性质，对列也成立。
性质 2：两行互换，值变号。推论：两行（列）相等，$D=0$。
性质 4：某一行都乘以 $k$，等于用 $k$ 乘以 $D$。

\[\left|\begin{array}{ccc} 1 & 2 & 3 \\ 4 k & 5 k & 6 k \\ 7 & 8 & 9 \end{array}\right|=k\left|\begin{array}{lll} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array}\right|\]

性质 5：两行对应成比例 $D=0$。
- 两行相等。
- 某一行全为 $0$。

1.3 行列式按行展开 49:21

行列式按行（列）展开
异乘变零定理
行列式相乘定理

1.4 行列式的计算（一） 33:30

1.4 行列式的计算（二） 51:06

1.5 克莱姆法则 17:36

n 个方程，n 个未知量。求解方程组。

齐次，方程个数等于未知量个数，D 不等于 0，只有零解。
齐次，有非零解，等价于 D 等于 0。

note

2.1 矩阵概念 36:44

x	行列式	矩阵
本质	一个数	数表
符号	\|\|	()[]
形状	方的	没要求

绵绵用力，久久为功。 迷茫、痛苦、失落、受挫、想速成，这些都是正常的，你想做成一件事，心里的渴望和现实的进展之间有了冲突，自然会产生这样的感觉。对于普通人来说，没啥办法，只能是硬磕，一点一点啃，去下笨功夫，根本没有别的办法，等你挺过去了，这些东西就是你的壁垒，别人的高墙。

2.2 矩阵运算（一） 58:47

矩阵提公因子，所有元素，外提一次。
行列式提公因子，一行提一次。

2.2 矩阵运算（二） 32:23

\[(A B)^{\top}=B^{\top} A^{\top}\] \[\left(A_1 A_2 A_3 A_4\right)^{\top}=A_4^{\top} A_3^{\top} A_2^{\top} A_1^{\top}\]

2.3 特殊矩阵 30:47

2.4 逆矩阵（一） 45:30

伴随矩阵：按行求按列放。

任意方阵都有伴随矩阵。

\[\left|A^*\right|=|A|^{n-1}\]

2.4 逆矩阵（二） 1:20:03

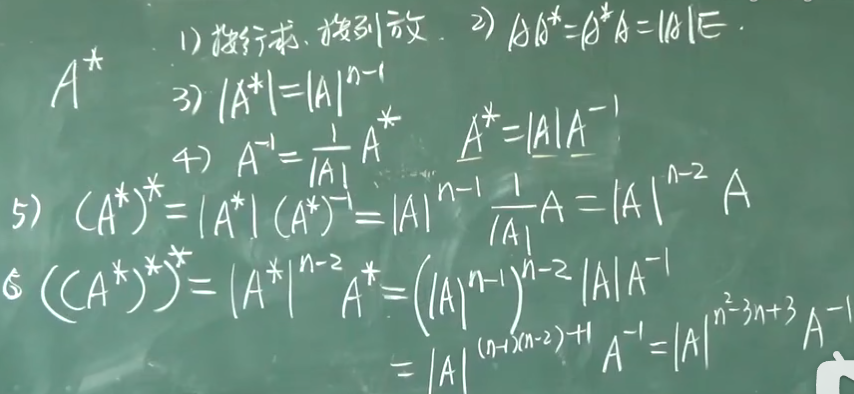
2.5 分块矩阵 40:47

2.6 初等变换（一） 41:48

2.6 初等变换（二） 1:00:56

左乘行变换，右乘列变换。

真是妙蛙种子吃妙脆角回米奇妙妙屋，妙到家了。

2.6 初等变换（三） 32:28

初等行变换。

\[(A, E) \stackrel{\text { 行 }}{\longrightarrow}\left(E, A^{-1}\right)\]

2.7 矩阵的秩（一） 13:10

秩：非零子式的最高阶数。

而这样推广出来的 —— 就是矩阵的秩序 —— —— 一个描述方程组是否拥有解出未知数组的值的能力。

学到后面的最大线性无关组就容易理解秩了。

2.7 矩阵的秩（二） 1:01:18

行简化阶梯型：

折线判断阶梯型
圆圈画出首非零元
竖线画首非零元是否为 1

阶梯型矩阵的秩等于非零行的行数（其他矩阵可以用初等变换化为在不改变秩的情况下阶梯型）

3.1 n 维向量及其运算 25:21

3.2 向量间的线性关系（一） 28:03

看了一晚上的泛函分析，感觉自己好幸运，没有读到数学专业，一定要更加努力工作，毕竟计算机还是可以勉强应付的。本来以为考过就好，结果毕业上班，什么线性代数、微积分、概率论，一个也逃不掉，毕业了工作十年翻开大学书慢慢看。最特别的应该是线性代数，行列式不知所云，学了图形学、图像处理、3D 渲染，齐次矩阵、矩阵的秩，再回头看，感叹发明这玩意的就是个天才。曾经有那么一个时刻，把支持向量机理论看懂了，过了几天，嘿 ;-) 又看不懂了。

3.2 向量间的线性关系（二） 52:02

整体无关 => 部分无关部分相关 => 整体相关增加向量个数，会提高线性相关的“可能性”

正交非零的向量必无关（正交的两个向量的乘积为 0）
属于不同特征值的特征向量一定线性无关

3.2 线性相关线性无关 23:09

$\boldsymbol a_1,\boldsymbol a_2,\cdots,\boldsymbol a_m$ 是 $m$ 个向量。

对于方程 $\lambda_1\boldsymbol a_1+\lambda_2\boldsymbol a_2+\cdots+\lambda_m\boldsymbol a_m=\boldsymbol0$，若其有非零解 $(\lambda_1,\lambda_2,\cdots,\lambda_m)\not=\boldsymbol0$，则称 $\boldsymbol a_1,\boldsymbol a_2,\cdots,\boldsymbol a_m$ 线性相关；

若其只有唯一解 $(\lambda_1,\lambda_2,\cdots,\lambda_m)=\boldsymbol0$，则称 $\boldsymbol a_1,\boldsymbol a_2,\cdots,\boldsymbol a_m$ 线性无关。

由此可见，$\boldsymbol0$ 向量和任意向量线性相关。

数学意义：看他们是不是可以组成一个 0
几何意义：看向量是否可以相互抵消
物理意义：看力是否可以相互抵消

α1,α2 相关 $<=>$ α1,α2 共线 α1,α2,α3 相关 $<=>$ α1,α2,α3 共面反之亦然

无关的向量组，接长向量组也无关。
相关的向量组，截短向量组也相关。

3.3 向量组的秩（一） 20:48

3.3 向量组的秩（二） 35:39

行秩 = 列秩 = 矩阵的秩 r(A) 完成。

4.1 线性方程组 10:37

消元：

交换两方程
用非零数乘某方程
某方程的 $l$ 倍加到另一方程

4.2 线性方程组有解判定 1:09:17

4.3 齐次方程组的解 28:16

4.4 方程组解的结构（一） 54:26

4.4 方程组解的结构（二） 45:32

又学了一遍《线性代数》，以前应试教育，都不知道自己学的啥玩意，这些年学了《图形学》《机器学习》等课程，再回头，这不都是同一个玩意吗。

上个视频 32 分钟的错误更正 01:24

5.1 矩阵的特征值与特征向量（一） 23:43

完成。

5.1 矩阵的特征值与特征向量（二） 45:49

n 阶对角型矩阵的特征值是主对角线上的元素。

5.1 特征值和特征向量的性质 1:18:25

线代得有几何直觉才能真正理解。

是一个特征值对应多个特征向量，一个特征向量对应一个特征值。

互不相同的特征值对应的特征向量，不论这些特征值中一个对应多少特征向量，只要这些特征向量接在一起，它们仍然是线性无关的。

入是 A 的特征多项式的 k 重特征值，A 的对应入的线性无关的特征向量最多是 k 个。 k 重特征根对应的线性无关的特征向量的个数 <=k。

教材就搞笑，培养人工计算器。 https://www.bilibili.com/video/BV1e54y1b7CA/ 行列式（二维）对应面积放大倍率。 秩的意义：矩阵变换后的空间维度。矩阵列向量所张成空间的维度（基向量个数）。

特征向量是在该矩阵上扩大一定倍数还和原来向量共线的向量。

A 星星的行列式的更正 01:35

完成。

5.2 相似矩阵和矩阵可对角化的条件 1:06:14

常用的可逆变换有：等价、相似、合同。

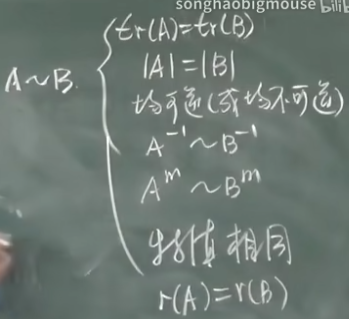
相似 & 相似对角形。

相似性的核心在于 —— 让矩阵变得尽可能简单但同时保留它的必要属性。

5.3 实对称矩阵的对角化（一） 26:46

内积，点乘。

向量的长度（范数，模）。

\[\|\alpha\|=\sqrt{(\alpha, \alpha)} .\]

正交，垂直。

正交向量组，不包含零向量。

5.3 实对称矩阵的对角化（二） 35:44

施密特正交化。就是减去别的维度的投影。其实是一个向量减掉在其他向量上的投影，剩下的向量就会垂直于其他向量。在用这些基底向量线性表示某个向量以后，基底向量前面的系数就是这个向量在这些基底向量张成的空间下的坐标。

5.3 实对称矩阵的对角化（三） 1:03:41

正交矩阵。 A 的 n 阶方， $A^{\top} A=E$。

如果有 n 阶矩阵 A，其矩阵的元素都为实数，且矩阵 A 的转置等于其本身（aij=aji），（i,j 为元素的脚标），则称 A 为实对称矩阵。

实对称矩阵 A 的不同特征值的特征向量正交。

n 阶实对称矩阵 A 的每个特征值 $\lambda_i$ 的重数 ki 等于对应的 $\lambda_i$ 的线性无关特征向量的个数。

6.1 二次型定义 57:46

6.2 二次型化标准型（配方法） 18:52

6.2 二次型化标准型（初等变换法和正交替换法） 36:48

惯性定理：任意一个二次型都可以通过非退化的线性替换化成规范形。

相同的正惯性指数，相同的负惯性指数，相同的秩。

6.3 有定性 16:20

有定的：正定、半正定、负定、半负定。

6.3 有定性的判别 29:28

顺序主子式。

7.1 线性空间 17:14

7.2 基、维数、坐标 22:51

参考资料快照

机器学习的数学基础系列文章

参考资料快照

本文短链接：
If you have any questions or feedback, please reach out